Tangent in Day-to-Day Life Situations

“To touch” is what the term “tangent” signifies. “Tanager” is the Latin word for the same thing. A tangent is a line that intersects the circumference of a circle precisely at one point but never enters the inside. Many tangents can exist in a circle. They run parallel to the radius. In this essay, we will study more about the tangent meaning and theorems. The tangent of an angle is the ratio of the opposite side’s length to the adjacent side’s length in trigonometry. In other words, it is the ratio of an acute angle’s sine and cosine functions such that the cosine function’s value does not equal zero. In trigonometry, the tangent function is one of the six fundamental functions.

A tangent is a line that is formed from an external point that goes through the point on a curve in geometry. Let’s use an example to better explain the concept of a tangent. An arc S and a point P outside of S are shown in the diagram below. A tangent has been made from P to S. This is an example of tangent representation.

Tangent Definition

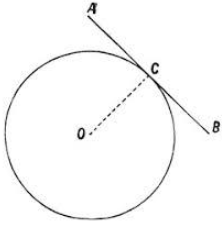
 In geometry, a tangent is a line that intersects a curve or curved surface at exactly one point.

Tangential Characteristics

The tangent has two key characteristics:

• Only one point on a curve is touched by a tangent.

• A tangent is a line that never passes through the centre of the circle.

• At the point of tangency, the tangent makes a right angle contact with the radius of the circle.

Aside from the qualities stated above, a tangent to the circle is related to mathematical theorems, which are utilised in major calculations in geometry.

Theorems of Tangents

On the tangent of a circle, there are two essential theorems. The two tangents theorem and the tangent to radius theorem are those. Let’s take a closer look at their claims and evidence.

The theorem states that the radius of the circle is perpendicular to the tangent drawn through the point where the radius meets the circle.

Application of Tangents

Science and Technology Tangent Applications

Tangent has a wide range of applications in science and technology because it is a function of both Sine and Cosine functions. Trigonometric functions are widely employed in the fields of engineering and physics. When something has a circular shape or resembles a circle, the sine, cos, and tan functions are expected to appear in the description. The following are some examples of notions that make use of trigonometric functions:

• Neural Networks (Artificial)

• Heuristic functions and empirical formulas

• Illustrations (Example: Andrews Plot)

• Elementary Particles and Their Behavior

• Waves such as sound waves and electromagnetic waves are studied.

Application of Tangents in real life

• The use of tangents in everyday life can be seen in the architecture that surrounds us. The tangent is represented by the width and height of a building. A school building, the Statue of Liberty, bridges, monuments, and pyramids are all instances of tangents in daily life.

• When a cycle travels down a road, the road becomes tangent at each location where the wheels roll.

• A tangent of a circle is also an abstract composition with a yellow ball and curb positioned tangentially on a stone background with the projection of the spherical shadow.

• A stone will follow a circular path if it is tied at one end of a string and turned from the other end. If we halt the motion abruptly, the stone will move in a tangential direction to the circular motion.

Tangency Concepts

The tangent is only considered when it intersects a curve at a single point; otherwise, it is simply a line. Based on the point of tangency and its location in reference to the circle, we may define the conditions for tangent as follows :

• When a point falls within the circle

• When a point falls within the circle

• When a point is outside the circle, it is said to be outside the circle.

Conclusion

The circle is only intersected by one point on the tangent. The line that passes through the point of contact and contains the radius is referred to as ‘normal’ to the circle at the point. The tangent is perpendicular to the radius of the circle that it traverses.