Profile
Settings
Refer your friends
Sign out
Data is a set of facts, usually in the form of numbers such as measurements or statistics. A data set is a collection of information that is commonly represented visually, such as in a table or graph. What exactly does data dispersion imply? The form of a data set when presented on a graph, most commonly a bar graph, is referred to as the distribution of data. A data set’s distribution can take many various forms, including symmetric and skewed. What is the definition of a symmetric data distribution? A symmetric distribution is a data visualization that appears virtually identical on both sides. It’s worth noting that the data doesn’t have to be identical on both sides to be termed symmetric; it only has to be close. Consider a mirror positioned in the midst of data distribution. Both sides should be almost exact replicas of one another.
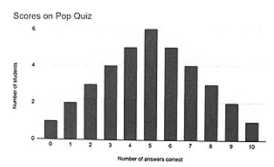
In the example below, a symmetric data distribution is depicted as a symmetric bar graph. The graph depicts the number of questions properly answered on a pop quiz by a hypothetical class of pupils.
The scores, in order from lowest to highest, are 0, 1, 1, 2, 2, 2, 3, 3, 3, 3, 4, 4, 4, 4, 4, 5, 5, 5, 5, 5, 5, 6, 6, 6, 6, 6, 7, 7, 7, 7, 8, 8, 8, 9, 9, 10.The graph’s two sides mirror, or nearly mirror, each other. The graph’s apex is smack dab in the middle. There was almost the same number of pupils who scored above and below the peak. The mean, median, and mode will all occur at the same position in a symmetric data set, which is crucial to know. In a symmetric data collection, the mean, or average, median, or exact middle number, and the mode, or most common number, will all be the same.
Consider the bar graph of the pop quiz results displayed above once again. The data set’s mean, median, and mode all fall on the number 5, indicating a symmetric distribution.
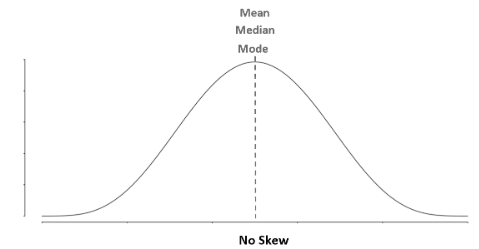
Properties of Symmetric Distributions
In a symmetrical distribution, the mean, median, and mode are all equal.
Remember the meanings of each of the following terms:
- Mean: This is the average of the values.
- Median: The value in the midway.
- Mode: The value that appears the most frequently.
Each of these numbers is equivalent to the other in a symmetrical distribution.
We’ve used unimodal distributions as examples in each of the previous instances – distributions with only one “peak.” A distribution can, however, be bimodal and symmetrical.
A binomial distribution is a distribution that has two peaks.
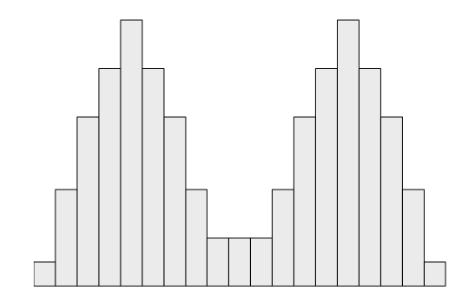
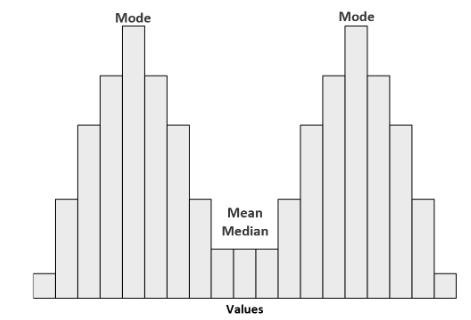
The left and right sides of this distribution would still mirror each other if we drew a line along the middle.
The mean and median of these distributions are the same. The mode, on the other hand, is found between the two peaks.
Symmetric Distributions & The Central Limit Theorem
The central limit theorem, which asserts that if the sample size is high enough, the sampling distribution of a sample mean is nearly normal, even if the population distribution is not normal, is one of the most significant theorems in statistics.
Sufficiently big sample size is required to apply the central limit theorem. The exact figure for “sufficiently big” turns out to be dependent on the underlying form of the population distribution.
Specifically:
- When the population distribution is symmetric, a sample size of 15 might occasionally be adequate.
- If the population distribution is skewed, a sample size of at least 30 people is usually required.
- A sample size of 40 or more may be required if the population distribution is significantly skewed.
As a result, when using the central limit theorem to calculate confidence intervals or perform hypothesis tests, we may use lower sample sizes with symmetric distributions.
Conclusion
A symmetrical distribution occurs when the values of variables appear at irregular frequencies and the mean, median, and mode appear at distinct locations. Skewness is a property of an asymmetric distribution. When shown on a graph, a Gaussian or normal distribution is curved like a bell curve, and the two sides of the graph are symmetrical.
In contrast to asymmetrical distribution, symmetrical distribution occurs when variable values exist at predictable frequencies and the mean, median, and mode are all present at the same time. A typical example of symmetrical distribution is the bell curve. The left and right sides of the curve would be mirror copies of each other if you drew a line along the centre. A fundamental idea in technical trading, symmetrical distribution posits that an asset’s price movement will follow this distribution curve over time.
