When a series of numbers is arranged to progress to a constant ratio with its succeeding term, it is called an arithmetico geometric series or simply the G.P series. The constant ratio at which the series progresses is called the series’s common ratio (r). The common ratio is calculated by dividing the succeeding term with the preceding term of the G.P. The sum of the first n terms of a G.P. is calculated using the summation formula. This article contains the sum of the G.P series with the help of arithmetico geometric series examples.
Arithmetico Geometric Series
Arithmetico Geometric Series or G.P series is a series of numbers where no term is equivalent to zero, and the subsequent terms are in a constant ratio. This series advances with a constant ratio.
Let us understand the concept by the following arithmetico geometric series examples,
Consider a series of numbers,
3, 6, 12,….
In the given series,
a1 = 3, a2 = 6, a3 = 18,
And, the ratio of the subsequent terms,
a2/a1= 6/3 = 2,
a3/a2 = 12/6 = 2,
Therefore, we can conclude that the series progresses with a constant ratio of 2; this constant ratio of a G.P series is called the common ratio and is denoted by r.
The Sum of nth Terms of a G.P Series
The sum of n terms of an arithmetico geometric series can be calculated using only the first term (a) and the G.P series’s common ratio (r).
The following formula is derived for the calculations of nth terms of an arithmetico geometric series,
S = a.(rn – 1) / (r – 1), or,
S = a.(1 – rn) / (1 – r).
This is the formula for the sum of the nth term of an arithmetico geometric series.
Now, let us understand how we get this formula.
Consider an arithmetico geometric series with the first term a and common ratio r. Let us consider S as the sum of n terms of this G.P series,
We know, a standard G.P series is given as,
S = a + ar + ar2 + ar3 + … + arn-1 …(i)
Now, let’s consider the value of r is 1, r =1,
S = a + a + a + a + … + a
S = an.
When r ≠ 1, multiplying r with equation (i),
We get, r.S = ar + ar2 + ar3 + ar4 + … + arn … (ii)
Now, subtracting equation (ii) from equation (i), we get,
(1 – r) S = a – arn
Or, (1 – r) S = a(1 – rn )
Finally, S = a(1 – rn) / (1 – r), or S = a(rn – 1) / (r – 1).
Solved Examples
Let us take some arithmetico geometric series examples and understand how to solve these problems,
Example: Find the result obtained by adding the first 11 terms of a G.P series, with the first term a and common ratio r, 5 and 4, respectively.
Solution: In this question, the G.P series first term and the common ratio is:
a = 5, r = 4,
The sum of n terms of a G.P series is given by,
S = a(r11 – 1) / (r – 1),
Implying the values in the formula,
S = 5.(411 – 1) / (4 – 1)
S = 5.(4194304 -1) / 3
S = 20971515 / 3
S = 6990505
Then the sum of the first 11 terms of a G.P series with first term 5 and common ratio 4 is 6990505
Example: Find the result obtained by adding the first ten terms of the following arithmetico geometric series,
3, 3/2, 3/4,…,
Solution: The given G.P series is,
3, 3/2, 3/4,…,
The common ratio of the G.P is,
a2 / a1 = (3/2) / 3 = 1/2
The first term of the series (a) is,
a = 3,
The sum of the n terms of a G.P is given by,
S = a.(1 – rn) / (1 – r),
For the given series,
S = 3.[1 – (1/2)10] / [1 – (1/2)]
S = 3.(0.9990 / 0.5)
S = 5.994,
Or, S = 5994 / 1000.
Example: Determine the result obtained by adding the n terms of the series mentioned below
6, 66, 666, 6666,….
Solution: The given series is not a G.P series; however, it can be written in the following form,
S = 6 + 66 + 666 + 6666 + …. to n terms,
S = 6 ( 1 + 11 + 111 + 1111 + … to n terms)
Or, S = 6/9. (9 + 99 + 999 + 9999 + … to n terms)
Or, S = 6/9. [ (10 – 1) + (102 – 1) + (103 – 1) + (104 – 1) + … to n terms]
S = 6/9. [ (10 + 102 + 103 + 104 + …n terms)] – [(1 + 1 + 1 + …n terms)]
Now we get two G.P series,
The formula for the sum of n terms can be given as
S = a.(rn – 1) / (r – 1),
We get,
S = 6/9. [ 10.(10n – 1) / (10 -1) – n]
Or, S = 6/9. [(10.(10n – 1) / 9)] – n
Therefore, the sum of n terms of the given series is,
6/9. [ (10.(10n – 1) / 9)] – n.
Conclusion
An Arithmetico Geometric Series is a series that progresses with a constant ratio; it can be a finite or infinite series of numbers.
The common ratio of the G.P series is defined as the ratio between two subsequent terms of the G.P series.
The sum of the nth term of an arithmetico geometric series is given by a formula, denoted by S; the formula is obtained by evaluating a standard G.P equation.

Binomial theorem for positive integral indices
According to the binomial theorem, the total number of terms in an expansion is always more than the index. Take, for example, an expansion of (a + b)n with n+1 terms and n as the index of the equation (a + b)n, where n is any positive integer.
The binomial theorem can be used to extend (x + y)n, where n is any rational number. Let’s look at the binomial theorem for positive integral indices.
The binomial theorem is a rule that can be used to enlarge any power of a binomial.

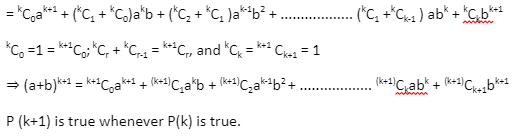
Therefore, P(n) is true for all positive integral values of n.
Properties of binomial theorem
- In the binomial expansion of (x+y)n, the number of coefficients is (n+1).
- In the expansion of (x+y)n, there are (n+1) terms.
- xn and yn are the first term and last term respectively.
- The powers of x decrease from n to 0 as the expansion advances, whereas the powers of y increase from 0 to n.
- The (r +1)th in the general term of of expansion is (x + y) n, which may be written as Tr+1=nCr xn-ryr.
- The coefficients of binomial expansion are organised into Pascal’s triangle.
- The nth term from the end of (x-y)n equals the (n-r+2)th term from the beginning in binomial expansion.
- The middle term in (x + y)n is (n/2)+1 if n is even; however, if n is odd, the middle terms are (n+1)/2 and (n+3)/2.
Coefficient of binomial theorem
The binomial coefficients are the figures associated with the variables x, y, in the expansion of (x +y)n. The binomial portions are represented as nC0, nC1, nC2. The binomial coefficients are attained through the Pascal triangle or by using the combinations formula.
Conclusion
The binomial expansion has more application than algebra II. In statistics, it is used to calculate the binomial distribution.
This allows statisticians to quantify the risk of a certain number of positive results in a set of trials.
Binomial expansion is also intriguing from a fine perspective as it allows mathematicians to gain insight into the properties of polynomials.
Binomial developments are used in numerous numerical and logical calculations, including kinematic and gravitational time enlargement, active energy, electric quadrupole post and determining the relativity factor gamma, to mention a few.
The number of terms in a binomial expansion of a binomial articulation raised to some power is another factor of the binomial development.
 Profile
Profile Settings
Settings Refer your friends
Refer your friends Sign out
Sign out






