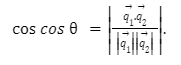Straight lines in 3D

A straight line is a line with infinite length without any width and curves on it. A simple, straight line on a plane has an equation:

y=mx+c

Here the slope of the line is represented by m.

A straight line in 3D can be exclusively determined only if it flows through two known points or it has been progressing through a single point but in a certain direction. The equations of such lines in 3D are usually determined in two forms, vector form and Cartesian form. There are many other forms for the equation of a line, such as equation of a line progressing through two known points, equation of a line when parallel to a vector and coursing through a single known point. We will also discuss the angles formed by two lines, the intersection point of the given lines etc.

Equation of a line flowing through two known points

Vector form- Let’s consider two points on a line as P and Q having position vectors p and q and take one more random point on a line as Y with position vector r. Considering all the above things, the line’s equation can be written as 

r=p+c(q-p)

Here c is some constant that is a real number.

Cartesian form- Let’s consider two points P and Q on the line having coordinates (x1,y1,z1) and (x2,y2,z2) respectively. Taking into account the above mentioned information, the line’s equation can be represented as 

Equation of line flowing in a definite direction and coursing through a single point

Vector form- Let’s consider a line flowing through a point P having position vector p and is parallel to a known vector q. Consider one more random point A having position vector r, the line’s equation will be 

r=p+cq

Here c is some constant that is a real number.

Cartesian form- Let’s consider a line flowing through a point P with coordinates (x1,y1,z1) and its direction ratios seems to be a, b, and c. Now, the line’s equation can now be written as

If we consider l, m, and n as the direction cosines of the line, the equation of the line will be

x-x1l=y-y1m=z-z1n

The point where the two straight lines in 3D intersect

Vector form- Let’s consider two lines as

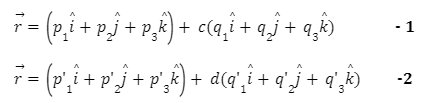
Now, if both these equations are intersecting at some point, then they must have a common point.

We will compare both equations to get three equations. We will use two of them to find the values of c and d first and we will check whether the values are satisfying the third equation or not. If it satisfies the third equation, the two lines intersect at some point and to find that points, we can simply just put the values of these two constants c and d in equations 1 and 2.

It can be done similarly for the Cartesian form: we just have to take the equations in Cartesian form and then solve them following the above procedure.

Angle between the two straight lines

Let’s consider two lines l1 and l2 and consider the acute angle between them.

Vector form- Let the equations for the lines l1 and  l2 be r=p1+cq1 and r=p2+cq2 respectively, where c and d are two scalars. Now, the angle between these two lines can be represented as

Cartesian form: Let the equations for the lines l1 and  l2 be x-x1a1=y-y1b1=z-z1c1 and x-x1a2=y-y1b2=z-z1c2  respectively. Here, a1,b1,c1and a2,b2,c2 are the direction ratios of the given lines. Now, the angle between the lines can be represented by

Conclusion

A straight line is a simple curve that can be extended indefinitely without any width. An equation of a straight line in 3D can be determined only if it is progressing through two given points or it is flowing through a simple known point in a certain direction. The line’s equation when coursing through one point and in a definite direction in vector form is r=p+cq and in Cartesian form it is . The line’s equation when flowing through two points in vector form is r=p+c(q-p) and in Cartesian form it is . We can even check if the two lines are intersecting and find their intersection point and also the angle between the two given lines.