Logic is the study of how to think logically. For example, to prove a theorem, we need to know how to evaluate the validity of a given argument.
Statement of operation
A valid statement is a declarative phrase that is either true or untrue, but not both. Otherwise, it is referred to as an erroneous claim. Small letters, such as p, q, r, etc., indicate statements.
Declarative Statements That Are Open And Compound
An open Statement of operation is a sentence that contains a variable that becomes a statement when specific values are assigned to the variable.
Compound statements are formed when two or more basic assertions are joined using words like “and,” “or,” “no,” “if,” “then,” and “if and only when.”
Values of truth and a truth table: Statement of Operation
The truth values of a statement are represented by the letters T and F and indicate whether a statement is true or untrue.
All potential values for the variables occurring in a compound statement are listed in a truth table, which summarizes the truth values of the resultant assertions.
Statement of operation in its simplest form
- Irregularity: The conjunction of p and q is a compound sentence created by two simple phrases, p and q using the connective ‘and’.
- Disjunction: The disjunction of p and q is a compound sentence created by two simple sentences, p and q using the connectives ‘or’.
- Refusal to acknowledge: A negation of a given assertion is a statement in which the truth value of a given statement is changed by employing words like “no” or “not.” In the case of statements, the statement’s negation is expressed by the abbreviation p.
- Sentence with a condition (Implication): p => q is the conditional sentence of p and q, which connects two simple sentences p and q by the phase, if and then.
- A Sentence with Two Conditionals (Bi-implication): The term “if and only if” connects two basic statements, and they are referred to as “biconditional sentences.” The symbol ‘=>’ is used to represent it.
Falsehood and Inconsistency: Statement of operation
The term “tautology” refers to a compound assertion that is true regardless of the value of any of its constituent parts. Conversely, a contradiction is a compound assertion that is wrong for every one of its components (fallacy).
Qualifiers and Qualified Term
There are two essential symbols in this phrase.
- The symbol may represent all values (‘). As a result, it’s called the universal quantifier.
- The sign (“) denotes the existence of something. An existential quantifier is a name given to the sign.
Statement with a Quantification
It is possible to refer to a quantified statement as an “open sentence with a quantifier.”
Quantified Statements Cannot Be Negated
- P(x) is true if and only if x is true .
- P (x) is indeed true when x is equal to A.
Contingencies: Statement of Operation
It’s possible to use truth tables to determine if a statement has a logical fallacy or is true. A tautology is a statement that is true in every row of the table. It’s a contradiction if it’s false in every row. There must be at least one row where the statement is true and at least one row where it is untrue for the proposition to be a contingency.
In light of this, what do you think?
If violets are blue and roses are red, then violets must be red as well.
Even though this may seem to be a contradiction, it is accurate. However, when it comes to logical characteristics, our intuitions are frequently incorrect. So, to figure out what kind of proposition it is, let’s represent it and build a truth table for it:
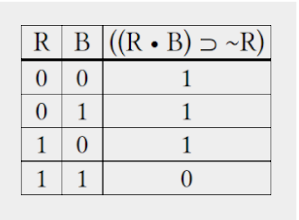
A look at the truth table above reveals that the statement is not a contradiction. True in every row except the final one: there are more ways to be true than there are ways to be false. It’s a contingency since it’s true in one row and untrue in another.
A few additional instances are in order. Here are the potential truth values for three compound propositions, as shown in the accompanying truth table. There is a tautology, a contradiction, and a contingency in each of these statements.
Is it possible to distinguish the difference?
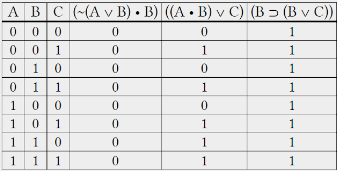
- In every row, the proposition (~(A ∨ B) • B) is a mistake because it is not true.
- There are some rows where ((A • B) ∨ C) is true, and others where it isn’t.
- (B ⊃ (B ∨ C)) is a tautology because it is true in every single row. Because it doesn’t have any zeros in
Instead, we may utilize the truth assignment technique to assess if a claim is a tautology, contradiction, or contingency for a Statement of operation. As an alternative to creating a full truth table, we may verify whether the proposition is false and if it is conceivable for it to be false.
Here’s a more detailed explanation of the Statement of operation:
- To decide whether a statement is a tautology, we must determine if the statement may be incorrect. Assuming you’re familiar with tautologies, here’s an example of one: Because the primary connective is supposed to be false, we begin by assigning “0” to that connective and then calculating the truth values of any additional connectives and sentences based on this assumption.
- Try all possible combinations of values for any letters that can’t be calculated to see if the proposition can be proven false. Tautologies are statements that cannot be refuted. Nevertheless, if you can discover a means to prove the statement to be untrue, you should move to the next step:
- Start by assigning “1” to the connective of the proposition, and then calculate any other connectives and sentence letters that can be determined based on the assumption that “1” is connective. Try every possible combination of values for those letters if they cannot be computed. A contradiction is a statement that can’t be true since there is no means to do it. However, it isn’t a paradox if you can discover a means to make the statement true.
- Steps 1 and 2 establish if a statement is a tautology or a contradiction; if it is neither, it is a contingency.
Conclusion
We have learnt about the Statement of operation. Truth-functional connectives cannot express the logical structure of certain propositions, and hence some tautologies and contradictions seem as if they are contingencies in propositional logic. In future chapters, we’ll cover a variety of logical structures.
 Profile
Profile Settings
Settings Refer your friends
Refer your friends Sign out
Sign out






