Watch Free Classes

A conic section (or simply conic) is a curve formed by the intersection of the surface of a cone with a plane in mathematics. The hyperbola, parabola, and ellipse are the three forms of conic sections; the circle is a sWhen a plane is parallel to the central axis of a cone, it touches both halves of the double cone, forming a hyperbola. Hyperbolas have two branches as well as the following characteristics:

  • Asymptote lines are two linear graphs that the hyperbola’s curve approaches but never touches.
  • The intersection of the asymptotes forms a center.
  • Each of the two branches bends around two focal points.
  • Each branch has two vertices.

The Standard form of equation of Hyperbola is

( x – h )² / a² – ( y – k )² / b² = 1

A hyperbola’s eccentricity is constrained to e > 1 and has no upper bound. When the eccentricity is allowed to reach +∞, the hyperbola degenerates into a straight line, which is a special case of the ellipse, though it is sometimes considered a fourth type. Conic sections are formed when a plane and a cone intersect. Nappes are two equally formed sections of a cone. One nappe is what most people think of when they say “cone,” and it resembles a party hat.

Important terms of Hyperbola

Focal Chord

A focal chord is a chord that runs through a focus.

Transverse Axis

The line joining the foci of the hyperbola is known as Transverse axis. The length of Transverse axis is 2a

Conjugate Axis

The axis perpendicular to the transverse axis is known as Conjugate axis. The length of Conjugate Axis is 2b

Double Ordinate

A double ordinate is a chord that is perpendicular to the transverse axis.

Conjugate Hyperbola

The conjugate hyperbola of a given hyperbola is the hyperbola whose transverse and conjugate axes are the conjugate and transverse axes of the provided hyperbola.

The equation of the conjugate hyperbola of the hyperbola x²/a² – y²/b² = 1 is 

  • x² / a² + y² / b² = 1

Points on the conjugate hyperbola can be expressed in coordinate geometry as ( a tanθ  , b secθ )

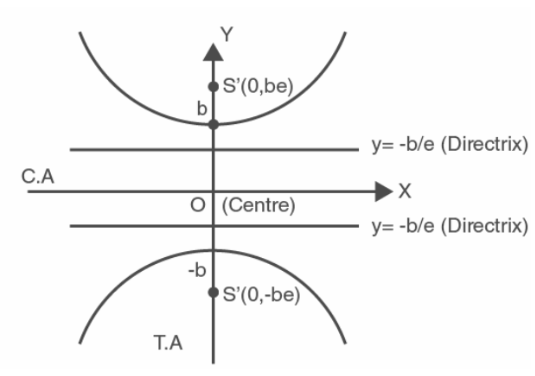
Properties of Conjugate Hyperbola

  • The equation of conjugate hyperbola is – x²/a² + y²/b² = 1 
  • It’s center is located at (0,0)
  • The vertices are located at (0,b) ; (0,-b)
  • The foci are located at (0,ae) and (0, -ae)
  • The length of the transverse axis of conjugate hyperbola is 2b.
  • The length of the conjugate axis of it is 2a.
  • The equations of directrices of conjugate hyperbola are x = b/e and x = – b/e.
  • The length of the latus rectum of the conjugate hyperbola is 2a² / b.
  • The eccentricity of conjugate hyperbola is e = √[1+ ( a² / b² )]
  • The equation of the conjugate axis of the conjugate hyperbola is y = 0.
  • The equation of the transverse axis of the conjugate hyperbola is x = 0.
  • The equations of hyperbolas and asymptotes differ by the same constant that separates the equations of asymptotes and conjugate hyperbolas.
  • Hyperbola + Conjugate hyperbola = A Pair of Asymptotes.
  • Tangents drawn at positions where a pair of conjugate diameters meet a hyperbola and its conjugates form a parallelogram, the vertices of which are on the asymptotes and whose area is constant.
  • If a pair of conjugate diameters of hyperbola meet the hyperbola and its conjugate in A, A’ and B, B’ respectively, then the asymptotes bisect AB and AB’.
  • If e1 and e1 are the eccentricities of the hyperbola and its conjugate then (1/e1² + 1/e2²)=1
  • Similar hyperbolas refer to two hyperbolas which have the same eccentricity.
  • The foci of a hyperbola and its conjugate are concyclic and form the vertices of a square.

Conclusion

The conjugate hyperbola of a given hyperbola is the hyperbola whose transverse and conjugate axes are the conjugate and transverse axes of the provided hyperbola. Points on the conjugate hyperbola can be expressed in coordinate geometry as ( a tanθ  , b secθ ). Hyperbola + Conjugate hyperbola = A Pair of Asymptotes. The eccentricity of conjugate hyperbola is e = √[1+ ( a² / b² )]. If e1 and e1 are the eccentricities of the hyperbola and its conjugate then (1/e1² + 1/e2)=1