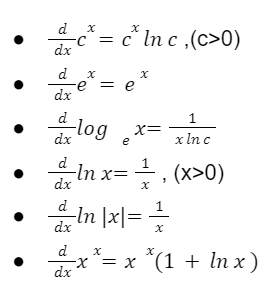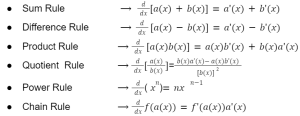Standard Derivatives

Differentiation is needed to find the rate of change. It all starts with the differentiation of a single variable to a higher order of variables. 

In a graph, it is indicated by the slope of a tangent line to the function at any point. Differentiation is applicable to several different variables. It can be done for implicit functions by taking the one in two variables as a variable and the other one as a function.

For example, the derivative of a function z = f(y), which means the rate at which the value of y changes with respect to the value of z.

The general representation of a derivative is d/dx.

For example, d/dy(1) = 0 

Which means differentiating 1 with respect to y gives 0 as a result.

Standard derivatives 

There are different kinds of derivatives and they fall under the following categories:

• Derivatives of simple functions
• Derivatives of trigonometric functions
• Derivatives of inverse trigonometric functions 
• Derivatives of logarithmic and exponential functions 
• Derivatives of hyperbolic functions
• Derivatives of inverse hyperbolic functions

Derivatives of simple functions

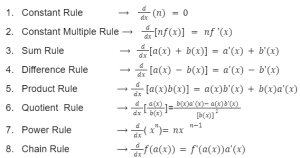
Derivatives of trigonometric functions

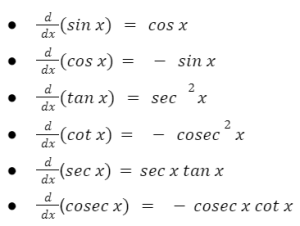
Derivatives of inverse trigonometric functions

Derivatives of logarithmic and exponential functions

Derivatives of hyperbolic functions

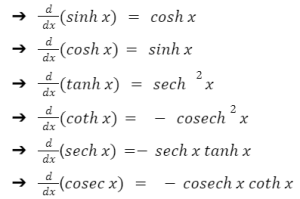
Derivatives of inverse hyperbolic functions

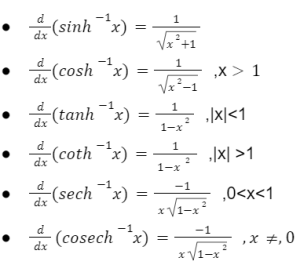
Derivatives of higher order

We saw derivatives of the 1st order and 2nd order respectively, but they do go on to the 3rd order, 4th, 5th upto the nth order. This is called the higher order of derivatives.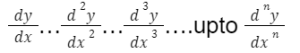                                  

Conclusion

The concept of standard derivatives and its related topics have been understood clearly now. Standard derivatives are an inevitable need in mathematics and our daily lives. Understanding the above derivatives helps a lot in solving different questions of any standard.