The ancient Greeks discovered ellipses when examining the conic section for the first time. When cutting the right corner at various angles, it formed an ellipse.
It occurs when a right circular cone intersects a plane, and a conic is essentially a form defined as the angle at which a plane intersects. Depending on the sign and coefficients, we can represent it as a set of points in the coordinate plane or as the graph of any quadratic equation in two variables.
An ellipse has two symmetry axes, called major and minor axes. The major axis ends at the ellipse’s vertex, and similarly, the minor axis ends at a co-vertex of the ellipse. The foci lie on the major axis, and the constant sum of the distances are always greater than the distance between them.
What is the general equation of an ellipse
The general equation of an ellipse is
x2 / a2 + y2 / b2 = 1
An ellipse’s centre may be anywhere, and its axes can’t be parallel to the coordinate axes. It results from starting with an ellipse in the standard position, then rotating and translating it. We may add zero rotations and zero vector translations in the most general formulation. Then we rotate and translate the ellipse to get every ellipse. We can get its equation by adding rotations and translations to an ellipse’s standard equation.
Rotate first, then translate. Let R represent rotation, and examine what happens to x = (x, y) if we first translate by vector v, then apply R. R is linear, hence R(x + v) = Rx + Rv. The same as rotating x first, then translating by Rv. It shows that a rotation followed by translation, or a translation followed by a rotation, may create any ellipse from one in the standard one. We’ll rotate, then translate to create a general elliptical equation.
(x, y) changed into (x cos α − y sin α, y cos α+x sin α) by a counter-clockwise rotation around the origin by an angle α. By rotating through 2π − α, we obtain the inverse operation, which transforms (x, y) into (x cos α + y sin α, y cos α − x sin α). Using the Transformed Ellipse method, we derive the following equation for a standard ellipse rotated by an angle α.
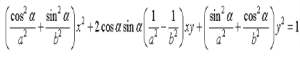 |
………………………… (1)
Expanding binomial squares and collecting terms provides
Ax2 + Bxy + Cy2 = 1 (A and C are positive). So the equation for a rotating ellipse with a nonzero xy term is quadratic.
Ax2 + Bxy + Cy2 = 1 is a quadratic equation. By factoring out y2, we get (At2 + Bt + C) = 1 / y2, where t = x / y is the reciprocal of the slope from the origin to the point (x, y). Except at the x intercepts, where y = 0. 1 / y2 is positive. While the point (x, y) traces the ellipse between the two x intercepts, it may take any real value. This shows that At2 + Bt + C = 0. Since At2 + Bt + C has no real roots, B2 − 4AC < 0. By computing readily verified this conclusion B2 4AC = 4 / (ab)2 using the coefficients in equation (1).
Ax2 + Bxy + Cy2 = 1 is always a rotating ellipse centred at the origin, and B2 4AC 0 is always positive. When you translate a curve by a fixed vector (h, k), you replace x with x h and y with y k in the equation for that curve. A (x − h)2 + B (x − h) (y − k) + C (y − k)2 = 1, where A and C are positive, B2 − 4AC < 0, and A and C are positive. E expanding the translated ellipse’s general form introduces x and y terms. The expanded version is
Ax2 + Bxy + Cy2 − (2Ah + kB) x − (2Ck + Bh) y + (Ah2 + Bhk + Ck2 − 1) = 0.
It shows that an ellipse’s equation is always a quadratic polynomial in x and y and that nonzero x or y terms imply a non-origin centre.
The perimeter of an Ellipse Formulas
The perimeter of an ellipse is the total length of its boundary in cm, m, ft, etc. The general formulas for calculating an ellipse’s perimeter are:
P ≈ π (a + b)
P ≈ π √ [ 2 (a2 + b2)
P ≈ π [ (3/2) (a+b) – √(ab)]
where,
a = Semi-major axis length
b = Semi-minor axis length
Area of Ellipse Formula
An ellipse’s area is the total area or region covered in two dimensions, measured in square units such as in2, cm2, m2, yd2, and ft2. For an ellipse, the major and minor axis lengths calculate the area. The area of an ellipse formula is:
Area of ellipse = π a b
where,
a = Semi-major axis length
b = Semi-minor axis length
The eccentricity of an Ellipse Formula
The eccentricity of an ellipse is the ratio between the distance between focus and the ellipse’s centre and the distance between one of the ellipse’s ends.
Eccentricity of the ellipse formula is e = ca=√1−b2a2ca=1−b2a2
Latus Rectum of Ellipse Formula
An ellipse’s latus rectum is the line perpendicular to the transverse axis and passing through its foci. Following is the formula for Latus Rectum of Ellipse:
L = 2b2/a
Properties of an Ellipse
- A plane intersecting a cone at its base forms an ellipse.
- Every ellipse has two foci, and the total of the distances between any two points on the ellipse is constant.
- Ellipses have major and minor axes.
- All ellipses have an eccentricity of less than one.
Conclusion
The ellipse is a necessary part of the conic section and has similar properties to a circle. The conic section includes the circle, parabola, ellipse, and hyperbola. The locus of a point with a fixed ratio is a conic section.
In comparison to circles, an ellipse has an oval shape. An ellipse has an eccentricity of less than one and represents the locus of any point whose lengths from the ellipse’s two foci are constant values. In daily life, simple examples of the ellipse include the shape of an egg in two dimensions, the running track in a sports stadium, a badminton racket, and planets’ orbits
 Profile
Profile Settings
Settings Refer your friends
Refer your friends Sign out
Sign out






