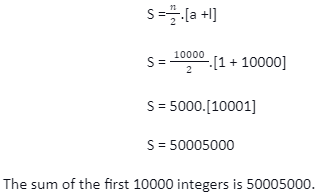Profile
Settings
Refer your friends
Sign out
The arithmetic progression series is the one that progresses with a constant value. The value at which an A.P series progresses is known as the series’ common difference (d). The arithmetic progression formulas do the calculation of the A.P series; these formulas are used to determine values such as the nth term of the series or the sum of n terms of the series. In the following article, we will look into some arithmetic progression formula examples.
Arithmetic Progression Examples
Let us understand the A.P series by looking at the following arithmetic progression formula examples.
Example 1
Find the first three terms, if the first term a, and the common difference of an A.P series are given.
- a = 2, d = 5
- a = 10, d = 10
- a = 100, d = – 5
Solution: In the first condition, the first term and the common difference of the A.P is given,
Example 2
Find the 10th, 21st, and 33rd terms of the following arithmetic progression series.
12, 24, 36, 48, 60,….
Solution: The given A.P series is,
12, 24, 36, 48, 60,…
The common difference (d) of the A.P series is,
d = 24 – 12,
d = 12.
The nth term of an A.P series is given by,
Example 3
Find the sum of the first 200 terms of the following A.P series,
8, 16, 24, 32, 40,….
Solution: The A.P series given is,
8, 16, 24, 32, 40,….
The first term (a1) and the common difference (d) of the A.P series are,
a = 8, d = 16 – 8 = 8.
The formula for the sum of n terms of an A.P series is given by,
Example 4
Find the sum of the first 10000 integers by using the A.P formula.
Solution: for the first 10000 integers, we get an A.P series in,
1, 2, 3,…., 10000.
Here, a = 1,
and, l = 10000.
Using the A.P formula we get,
Example 5
How many terms of the given A.P series, 6, 12, 18, 24,… must be taken, so their sum is 816?
Solution: The given A.P series is,
6, 12, 18, 24,…
Here, a = 6,
d = 12 – 6 = 6,
S = 816.
n = ?,
Using the formula,
Conclusion
The arithmetic progression series is calculated using different formulas like the formula for the nth term and the formula for the sum of an arithmetic progression series. The arithmetic progression examples explain how to solve various problems in the A.P series. These problems vary from finding the value of an unknown term to finding the sum of an A.P series. The arithmetic progression formula examples explain the calculation of d is done in an A.P and how an A.P is formed.
