Profile
Settings
Refer your friends
Sign out
A modulus function determines a number’s magnitude regardless of its sign. The absolute value function is another name for it. The modulus of a real number x is given by the modulus function, represented as |x| in mathematics. It returns a non-negative value for x, implying that the function’s output is always positive, regardless of the input. In this article, we will learn about the solved examples on modulus and its application with the help of some solved examples.
Modulus function
A modulus function is a function that returns a number or variable’s absolute value. It generates the number of variables’ magnitudes. A number’s modulus, or absolute value, is also known as the number’s distance from the origin or zero. Â
The function is denoted as y = |x| or f(x) = |x|,Â
where f: R → R and x ∈ R.
Â
f(x) = x,  if x ≥ 0       f(x) =-x,   if x<0
Therefore, in mathematics, |x| is the modulus of x, where x is a real number. If x is greater than or equal to 0, the modulus function returns the actual value of x. If x is less than 0, the function takes the minus of the actual value ‘x’.
Â
Calculation of modulus function
The modulus function’s application and calculation are simple to comprehend. As a consequence of the function, the modulus function always returns the absolute value of the input x.
To understand the application of the formula, let us consider a few solved examples:
Â
Solved example: Consider the modulus function f(x) = |x – 1|. Then:
- If x = -7, then y = f(x) = – (-7 – 1) = 8, since x-1 is less than zero
- If x = 5, then y = f(x) = 5 – 1 = 4, since x-1 is greater than zero
- If x = 1, then y = f(x) = – (1 – 1) = 0, since x-1 is equal to zero
Thus similarly, we can solve for any modulus function. However, we must also understand the intricacies of the domain and range of modulus functions before proceeding further.
Graph of modulus function meaning
The graph of modulus function depicts the relationship between x and y as x changes. The graph is drawn so that the range of function f(x) is positive for all x values.
Thus, for a function, y = |x|:
- The x-axis shows the value of variable xÂ
- The y-axis shows the value of function y.Â
Let us take a solved example for better understanding. Suppose x is a variable, and f(x) = |x|. Then, according to the function, the output of f(x) for changing values of x will be as follows:
Â
x | f(x) = |x| |
15 | 15 |
10 | 10 |
5 | 5 |
1 | 1 |
0 | 0 |
-1 | 1 |
-2 | 2 |
-3 | 3 |
-4 | 4 |
-5 | 5 |
Â
Thus, when these values are plotted on a graph, the graph of the modulus function f(x) = |x| will look like this:
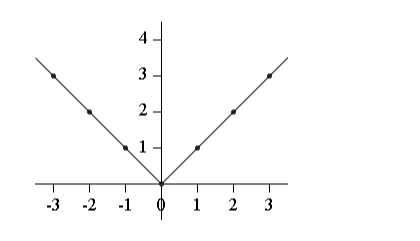
It can be seen from the graph that the relationship between x and y for function y = |x| is as follows
- If x = -5 then y = |-5| = 5
- If x = -4 then y = |-4| = 4
- If x = -3 then y = |-3| = 3
- If x = -2 then y = |-2| = 2
- If x = -1 then y = |-1| = 1
- If x = 0 then y = |0| = 0
- If x = 1 then y = |1| = 1
- If x = 5 then y = |5| = 5
- If x = 10 then y = |10| = 10
- If x = 15 then y = |15| = 15
Â
Thus it can be easily inferred from the graph that for all possible values of x, the function f(x) remains positive.Â
Solved Examples On Modulus
Question 1:
Solve |x + 4| = 10 using modulus function.
Solution:Â
As we have noted earlier, the modulus function always gives positive output. Therefore for the function |x + 4| = 10, there can be two situationsÂ
If x + 4 > 0, then |x + 4| = x + 4 and
If x + 4 < 0, then |x + 4| = −(x + 4)
Â
Situation 1: If x + 4 > 0
|x + 4| = x + 4
⇒ x + 4 = 10
⇒ x = 10 − 4 = 6
Â
Situation 2: If x + 4 < 0, we have
|x + 4| = − (x + 4)
⇒ − (x + 4) = 10
⇒ − x − 4 = 10
⇒ x = − 4 − 10 = − 14
Therefore, the solution for x is −14 and 6.
It can thus be said that −14 < x < 6.
Â
Question 2:
Solve x for |x2 – 7x + 12| using modulus function:
Â
Solution:
|x2 – 7x + 12| = |(x – 3) (x – 4)| = |f(x)|
Â
According to the definition of modulus function,
When f(x) is positive
|f(x)| = f(x)
When f(x) is negative
| f(x) |= -f(x)
Â
Thus,Â
f(x) = (x – 3)(x – 4) is non-negative or zero when x = (- ∞, 3] ∪ [4, ∞)
f(x) = (x – 3)(x – 4) is negative when x = (3, 4)
Â
So, |x2 – 7x + 12| = (x2 – 7x + 12) when x = (-∞, 3] ∪ [4, ∞) and
|x2 – 7x + 12| = -(x2 – 7x + 12) when x = (3, 4)
Â
Question 3:
If |x2 – 7x + 12| + |x2 – 9x + 20| = 0. Find x.
Â
Solution:
We know that a modulus function is always a positive number.Â
In the question, |x2 – 7x + 12| + |x2 – 9x + 20| = 0
Thus, when two different modulus functions add up to zero, then it must mean that both the modulus functions are also equal to zero (The sum of two positive numbers can never be zero unless they both are equal to 0).
Thus,Â
x2 – 7x + 12 = 0Â
(x – 3) (x – 4) = 0
x = 3, 4
Similarly,Â
x2 – 9x + 20 = 0
(x – 4) (x – 5) = 0
x = 4, 5
Â
Thus it can be seen that both the equations are zero at only one point, ie, when x = 4
Thus the only possible solution for x for |x2 – 7x + 12| + |x2 – 9x + 20| = 0 is x = 4
Conclusion
Thus in this article we have studied that the modulus of a real number x is given by the modulus function. The function provides a non-negative value for x, implying that the function’s output is always positive. We have also learnt how to plot the graph of the modulus function, which depicts the relationship between x and y.
