In some steps, both general and specific integration will be used to address the problem. With the help of solved examples, we will learn how to solve a differential equation. Learn how to solve first-order and second-order differential equations in general.
General solution of a differential equation
When the arbitrary constant of the general solution attains a unique value, the general solution becomes the specific solution of the issue.
The particular solution of a differential equation is obtained by employing the boundary conditions (also known as the initial conditions).
To achieve a specific solution, first a general solution is discovered, and then the specific solution is constructed utilising the specified conditions.
Suppose,
dy/dx = eˣ + cos2x + 2x³
Then we know what the overall answer is:
y = eˣ + sin2x/2 + x⁴/2 + C
Now, if we substitute x = 0 for y = 5 in the general solution, we get:
5 = e⁰ + sin(0)/2 + (0)⁴/2 + C
C = 4
As a result, if we substitute the value of C in the general solution, we get
y = eˣ + sin2x/2 + x⁴/2 + 4
General solution for first and second order
If we’re using the variable separable technique to solve a first-order differential equation, we’ll need to specify an arbitrary constant before we start integrating. As a result, following simplification, we can observe that a solution of the first-order differential equation has at least one fixed arbitrary constant.
Variable separable differential equation
Differential equations expressed in terms of (x,y) such as the x-terms and y-terms can be sorted to various sides of the problem in variable separable differential equations (including delta terms). As a result, following separation, each variable may be readily integrated to get the differential equation’s solution. The equations are as follows:
f(x)dx+g(y)dy=0
where f(x) and g(y) are x and y functions or constants, respectively.
A general solution of a second-order differential equation, for example, will consist of two fixed arbitrary constants, and so on. An m-parameter group of curves is geometrically interpreted by the general solution.
Particular solution of a differential equation
A Particular Solution is a differential equation solution that is derived from the General Solution by assigning specific values to the random constants. The requirements for obtaining the values of the random constants can be supplied to us as an Initial-Value Problem or as Boundary Conditions, depending on the question.
Hermite differential equation
The ordinary differential equation of second order



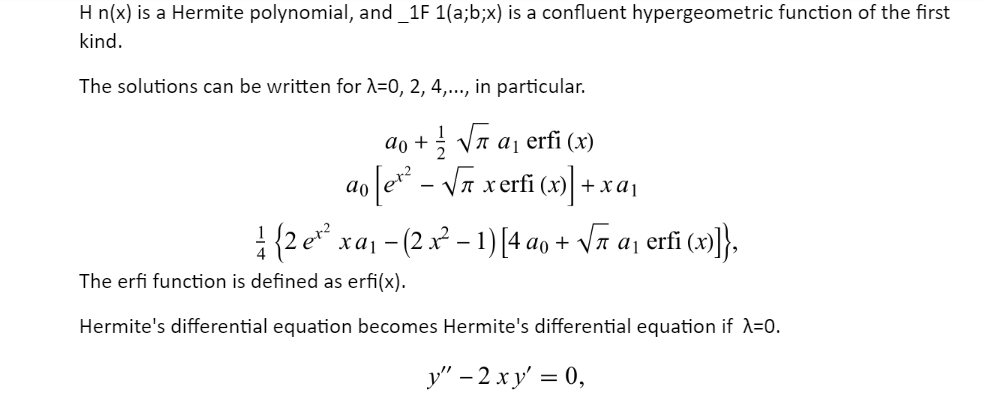
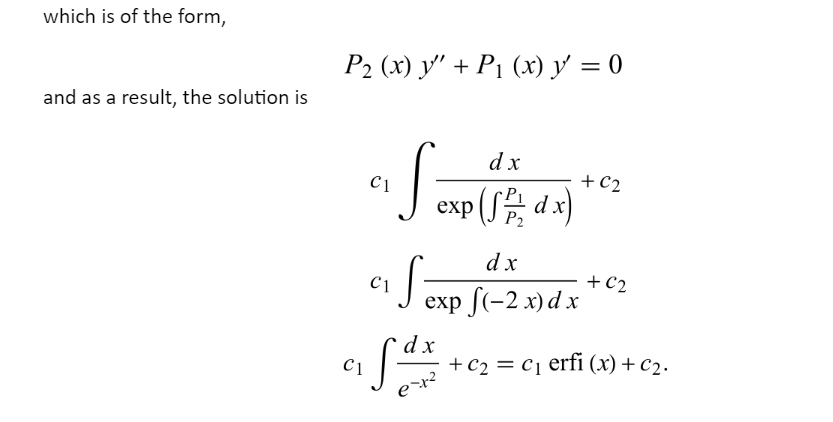
Implicit Function Differentiation
To find the derivative of an implicit function, you don’t need to know the formula. Indeed, it can be difficult to obtain the formula for an implicit function without first creating a different type of function: Consider the relationship cos y = x once more. Using implicit differentiation, we may calculate the derivative of the implicit functions of this connection where the derivative exists. Implicit differentiation is the concept of considering y as a function of x. Let us show this by rewriting the relationship above with y(x) instead of y:
i.e. cos(y(x)) = x
We now differentiate both sides of the equation and make their derivatives equal. Because we don’t know the formula for y(x), we’ll use y’(x) instead:
-sin(y(x)) · y'(x) = 1
Finally, we obtain the needed formula by solving for y’(x):
y’(x) = -1 /sin(y(x))
= -1/sin y
Conclusion
In real life, ordinary differential equations are used to compute the movement or flow of electricity, the motion of an object to and fro, such as a pendulum, and to illustrate thermodynamics ideas. They’re also used to visualise the course of diseases in graphical form in medical terminology.
 Profile
Profile Settings
Settings Refer your friends
Refer your friends Sign out
Sign out






