Skew Lines

Skew lines are defined as a pair of lines that are not parallel to one another and do not intersect with one another. Skew lines are only possible in spaces with dimensions greater than two-dimensionality. They have to be non-coplanar, which means that parallel lines must be found in more than one plane. In a space with only two dimensions, it is possible for two lines to either intersect or run parallel to one another. As a result, skew lines are impossible in a space with only two dimensions.

Skew lines are present in a variety of situations that occur in real life. Let’s say there’s a line painted on the wall and another line painted on the ceiling. Skew lines are lines that do not intersect and do not run parallel to one another; if these lines do not run parallel to one another, then they are not skew lines. These lines proceed indefinitely in both directions simultaneously. In the following paragraphs, we will go over what skew lines are, look at some examples of them, and discuss how to calculate the shortest distance between two skew lines.

What exactly are skew lines

Before we can move on to learning about skew lines, we need to first become familiar with the other three types of lines. These are presented in the following order:

Lines that cross each other at a particular point are known as intersecting lines. If two or more lines cross each other at a particular point, then those lines are known as intersecting lines and they lie in the same plane.

Lines that lie in the same plane but never cross each other are said to be parallel lines. This applies even if the lines are extended indefinitely; they still won’t touch.

Lines that are Coplanar Coplanar lines are lines that lie in the same plane.

Skew Lines Definition

Skew lines are a pair of lines that do not intersect with one another, do not run parallel to one another, and do not lie on the same plane. This indicates that skew lines cannot intersect at any point in time and that they are not parallel to one another. It is only possible for lines to exist in two dimensions or on the same plane if they either intersect or run in parallel with one another. Skew lines will never be coplanar due to the fact that this property does not apply to them; as a result, they will always exist in three dimensions or more.

Illustration of Skew Lines

In the real world, a single city may be comprised of several distinct types of roadways, such as highways and overpasses. These roadways are considered to be on separate planes of existence. The lines that are drawn on such roads will never intersect with each other and will not be parallel to one another, which will result in the formation of skew lines.

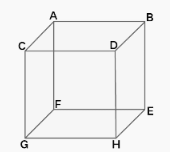
A Cube Containing Skew Lines

One example of a solid shape that can be represented in three dimensions is a cube. We will follow these three steps in order to locate skew lines in a cube.

The first thing you need to do is locate lines that do not cross each other.

Step 2: Determine whether or not the aforementioned pairs of lines are parallel to one another.

Step 3: After making sure that these lines do not intersect and that they do not run parallel to one another, check to see if they are coplanar. If the answer is yes, then the lines that have been selected are skew lines.

Let’s say we have a cube and its dimensions are as follows:

It is clear that lines CD and GF do not intersect and are not running in parallel with one another. In addition to this, they do not coexist on the same plane. Therefore, CD and GF are considered to be skew lines.

When searching for skew lines, it is also possible to include the diagonals of solid shapes.

A Formula for Skew Lines

In a space with only two dimensions, there are no skewed lines. Both the vector method and the cartesian method can be used to calculate the shortest distance between two skew lines in three dimensions, and we have formulas for doing so. The process of calculating the angle that exists between two skew lines is somewhat difficult due to the fact that these lines are not parallel and do not cross over one another.

The Angle That Is Created By Two Skew Lines

Take for example that we have two skew lines, PQ and RS. Create a point O on RS, and then name the line that you draw from this point OT so that it is parallel to PQ. The measure of the angle that exists between the two skew lines can be obtained by using the angle SOT.

Several Important Remarks Regarding Skew Lines

• Skew lines are lines that do not intersect with one another, do not run parallel to one another, and do not coplanar with one another.
• Skew lines are only able to exist in environments with three or more dimensions. As a result, skew lines are impossible in a space with only two dimensions.
• Both the vector form and the cartesian form are valid presentation formats for the formula that determines the shortest distance between two skew lines.

Conclusion

Skew lines are defined as a pair of lines that are not parallel to one another and do not intersect with one another. Skew lines are only possible in spaces with dimensions greater than two-dimensionality. They have to be non-coplanar, which means that parallel lines must be found in more than one plane. In a space with only two dimensions, it is possible for two lines to either intersect or run parallel to one another. As a result, skew lines are impossible in a space with only two dimensions.Skew lines are present in a variety of situations that occur in real life. Let’s say there’s a line painted on the wall and another line painted on the ceiling. Skew lines are lines that do not intersect and do not run parallel to one another; if these lines do not run parallel to one another, then they are not skew lines. These lines proceed indefinitely in both directions simultaneously.