Profile
Settings
Refer your friends
Sign out
In trigonometry, there are three major ratios on which trigonometric functions and formulas are built. One of these is the sine function. The ratio of the perpendicular (opposite side of the angle) to the hypotenuse is given by the sine function (sin) of an angle. In the same way, the inverse sine function (sin-1) calculates the angle’s hypotenuse to perpendicular ratio. The basic angles that are usually used are 0,30,45,60, and 90 degrees. They can also be written in radians as π/2, π/3, π/4, π/6, and so forth.
Sine function:
The sine function in trigonometry is defined as the ratio of the opposite side’s length to the hypotenuse’s length in a right-angled triangle. A right triangle’s unknown angles or sides are found using the sine function.
The sine function for any right triangle with an angle, say ABC, is:
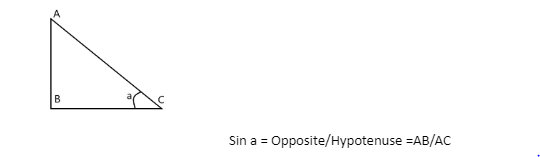
Properties of sine function as per quadrants:
Depending on the quadrants, the sine function yields positive or negative values. Sine 270 is negative, while sine 90 is positive, as shown in the table above. The value of the sine function is determined by the quadrants and is positive in the first and second quadrants, but negative in the third and fourth quadrants.
Sin 1:
0.8414709848 is the radian value of sin 1.
We have, π/3 = 1.047198 ≈ 1
Sin (π/3) = √3/2 and sin π = 0
We can now write using these data:
Sin 1 = sin[π/3-(π/3-1)]
Sin 1 = sin(π/3)cos(π/3-1) – cos(π/3)sin(π/3-1)
The angle (π/3-1) = 0.047198 is quite small.
For small angles, we know that,
Sin θ ≈ θ and cos θ ≈ 1
Therefore, sin 1 ≈ (√3/2 x 1)- [1/2 x (π/3-1)]
As a result, sin 1 = 0.8414709848
How to find the value of Sin 1?
The argument for the sine of an angle, say x, can be radian or degrees. Radian measurement is the rule.
Now we know that, π radian = 180 degree
Therefore, 1 rad = 180/π degree
1 rad = 57.2957795131
By taking in degree terms, we know that,
Sin 0° = 0 and sin 90° = 1
Also in radians,
Sin 0 = 0 and sin (π/2) = 1
Now, π = 3.14159265359, π/2 = 1.5707963268.
Thus, sin (1.5707963268) = 1, whenever the angle is in radian.
As a result, sin (1) = 0.8414709848 [angle in radian]
When angle is in degree, sin (57.2957795131) = 0.8414709848
Sine of 1 in terms of Π:
The inverse function of sin 1 is the angle whose sine is 1. The function sin 1 is equal to the sine of the angle 90°, which is 1. As a result, the inverse function of sin 1 is 90° or /2. It is the sine function’s maximum value.
Inverse sine function:
The inverse sine function, commonly known as arcsine, is the inverse of the sine function. The inverse of sine is denoted by the symbol (sine⁻¹). The angle’s value is calculated using the inverse sine function. (opposite side of angle/ hypotenuse) = sin⁻¹. Angle theta’s major branch value is. This means that theta’s value will be somewhere in the middle.
Value of inverse of sin 1:
The inverse sine function’s inverse sin of 1, sin⁻¹ (1), is a very uncommon value. The angle whose sine is x is given by Sin⁻¹(x). As a result, sin⁻¹ (1) equals the angle whose sine is one.
As we know,
Sin 90 = 1
Hence, sin ⁻¹ (1) = 90
Sin⁻¹ (1) = Π/2 (in radian)
Because the inverse sin⁻¹ (1) is 90 degrees or Π/2. The sine function’s maximum value is ‘1.’ As a result, it will happen at every 90 degrees, such as at Π/2, 3Π/2, and so on.
As a result of this, we can deduce:
Sin⁻¹ (1) = Π/2+2Πk (for any integer k).
Conclusion:
Triangular supports are used extensively in architecture and engineering. Trigonometry aids an engineer in calculating the correct angles when evaluating weight loads and bridge strength by determining the length of cables, the height of support towers, and the angle between the two. It also enables contractors to properly layout a curved wall, calculates the necessary roof slope, or determine the height and rise of a stairway. You may also use trigonometry at home to find the square footage of a curved piece of land without having to climb thousands of feet in the air.
