Watch Free Classes

By giving the value +1 to each positive input value and the value -1 to any negative input value, the Signum function may be used to identify the sign of a real value function. In the fields of physics, engineering, and artificial intelligence, where it is most commonly used for prediction, the signum function has several applications that may be explored. 

Let’s go more into the signum function, the graph of the signum function, and the many applications of the signum function. 

Definition of Signum Function

The sign for the specified x values is what is returned by the signum function. For x values that are more than zero, the output has a value of +1; for x values that are less than zero, the output has a value of -1; and for x values that are equal to zero, the output value is 0. 

A strange function that is distinct from the trigonometric function of the sine function is referred to as the signum function. 

Graph of a Signum Function

There are two horizontal lines that are drawn parallel to the x-axis on the graph of the signum function. These lines are located on opposite sides of the y-axis. A piece of the line that is placed in the first quadrant and is perpendicular to the positive x-axis acts as a representation for the outputs of all of the positive x values. This portion of the line serves as a representation for the outputs. You can find the output of the negative x-values in the third quadrant of the graph, which is represented by a section of the line that is parallel to the negative x-axis. This segment of the line represents the output.

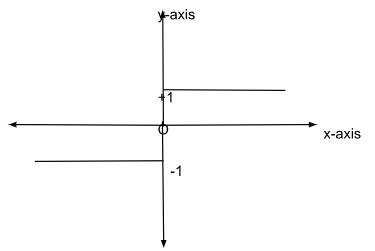
Domain of Signum Function

While the domain of a signum function is displayed on the x-axis and includes all real numbers, the range of a signum function is only comprised of two values and is shown on the y-axis. These values are +1 and -1. 

Application of Signum Functions

The signum function is useful in a variety of different areas of mathematics, including physics, engineering, and even daily life. The following is a list of the signum function’s applications that are considered to be some of the most significant. 

  • The signum function aids in the extraction of the real number’s sign.
  • When used to a complex number, the signum function aids in projecting it onto the unit circle.
  • A line inclined positively or negatively with the x-axis is obtained by integrating a signum function.
  • The use of probability in the context of a signum function predicts whether or not an event will occur.
  • Any of the on-off function switches can make use of the concept of signum function. The switches can be configured to turn on or off based on defined input values or input value fluctuation.
  • A thermostat is a good example of how the signum function is used. The system is turned on and starts cooling when it reaches a particular temperature, and it is turned off and stops cooling when it reaches a certain temperature.

Examples of signum function

  1. What would be the result for the values of x,by the signum function. x = {- 4.93, – 7.66, 12, 0, 4.2, 2.33333, -8.10}

Solution: Here we use the following signum function to find the output, for the input values of x.

 = {- 4.93, – 7.66, 12, 0, 4.2, 2.33333, -8.10}

Output = {-1,-1,+1,0,+1,+1,-1}

Conclusion:-

Calculus relies heavily on functions as its central building block in mathematics. The functions are distinguished from other types of connections by their particular nature. In mathematics, a function is conceptualised as a set of guidelines that each provide a distinct result for all input x. In mathematics, the expression of a function often involves the use of mapping or transformation. Typically, alphabets such as t, 9 and h are used to indicate functions. The signum function is used to assist in determining the sign of the real value function. It assigns the value +1 (positive 1) for positive input values of the function and assigns the value -1 (negative 1) for negative input values of the function. The signum function is used in a wide variety of contexts, including physics, engineering, and mathematics. It is also heavily used in artificial intelligence, specifically for forecasting.