Profile
Settings
Refer your friends
Sign out
Circular functions, sometimes known as trigonometric functions, can be simply described as functions of a triangle’s angle. This means that these trig functions determine the relationship between the angles and sides of a triangle. Sine, cosine, tangent, cotangent, secant, and cosecant are the basic trigonometric functions. A number of trigonometric formulas and identities define the relationship between the functions and aid in the determination of the triangle’s angles.
Six trigonometric functions:
The sine, cosine, and tangent angles are the fundamental classifications of trigonometric functions. The cotangent, secant, and cosecant functions can all be deduced from the basic functions. In comparison to the fundamental trigonometric functions, the other three functions are frequently used. Take a look at the diagram below for an explanation of these three major functions. The sin-cos-tan triangle is the name for this diagram.
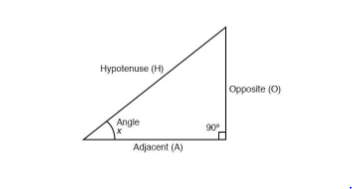
Sine function:
The ratio of the opposite side length to the hypotenuse is the sine function of an angle. The value of sin, as shown in the diagram, is
Sin a = Opposite/Hypotenuse
Cos function:
The cosine of an angle is the ratio of the neighboring side’s length to the hypotenuse’s length. The cos function can be calculated using the figure above.
Cos a = Adjacent/Hypotenuse
Tan function:
The tangent function is the ratio of the opposing side’s length to the adjacent side’s length. It’s worth noting that the tan can also be expressed as the ratio of sine and cos. The tan function will be as follows, as seen in the diagram above.
Tan a = Opposite/Adjacent
Tan can also be expressed in terms of sine and cos:
Tan a = sin a/cos a
Secant, Cosecant, and Cotangent functions:
The three supplementary functions secant, cosecant (cosec), and cotangent are derived from the main functions sine, cos, and tan. Cosecant (cosec), secant (sec), and cotangent (cot) are the reciprocals of sine, cos, and tan, respectively. Each of these functions has the following formula:
Sec a = 1/(cos a) = Hypotenuse/Adjacent
Cosec a = 1/(sin a) = Hypotenuse/Opposite
Cot a = 1/(tan a) = Adjacent/Opposite
Sign of trigonometric functions in different quadrants:
In the diagram below, the sign of trigonometric functions in each quadrant is shown.
All functions are positive in the first quadrant, only sin and cosec are positive in the second quadrant,
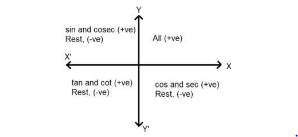
only tan and cot are positive in the third quadrant, and only cos and sec are positive in the fourth quadrant. As a result, the signs of various trigonometric functions in different quadrants can be tabulated as follows:
Example:
Find the value of cosec x if cot x = -5/12 and x lies in the fourth quadrant.
Solution:
Given,
Cot x = -5/12
We know that,
cosec²x – cot²x = 1
cosec ²x = 1 + cot²x
= 1 + (-5/12)²
= 1 + (25/144)
= (144 + 25)/144
= 169/144
cosec x = √(169/144) = ±13/12
Given that x is in the fourth quadrant and cosec x in the fourth quadrant is negative.
As a result, cosec x = -13/12
In the same way, we may easily solve a variety of trigonometry problems. These can be used to calculate the values of trigonometry functions that are dependent on other functions as well as trigonometry angles.
Conclusion:
The sign of a trigonometric function is determined by the coordinates of the points on the angle’s terminal side. You can figure out the signs of all trigonometric functions by knowing which quadrant the angle’s terminal side is in. The terminal side of an angle can be found in one of eight places: in any of the four quadrants, or along the axes in either a positive or negative direction (the quadrantal angles). For the signs of trigonometric functions, each scenario has a different meaning.
