What does the term “cross product” refer to?
Cross product is a two-vector, three-dimensional, binary operation. It creates a vector that is perpendicular to both vectors. a b represents the vector product of two vectors, a and b. Perpendicular to both a and b, the resulting vector is the same. This kind of product is known as a cross product. The right-hand rule is used to determine the cross product of two vectors.
Dot product and cross product are methods for multiplying two or more vectors. Let’s take a closer look at each of the vector products.
Cross Product with Right-Hand Rule
The right-hand rule may be used to determine the direction of the unit vector. Stretching our right hand in this manner, we can make sure that our index finger is pointing at our first vector, and our middle finger points toward our second. This is done by pointing with one’s thumb at one’s right hand’s nth finger. The right-hand rule makes it simple to demonstrate that the cross product of two vectors is not commutative. The right-hand rule diagram looks like this when we have two vectors A and B:
Dot Product
The scalar product of vectors is another name for the dot product, which is also known as the vector scalar. The scalar value of the dot product of the vectors is the resultant. The product of the magnitudes of two vectors and the cosine of the angle between them is known as the “dot product” of vectors. There are two vectors, and the consequence of their dot product is in the same plane as the two vectors. Positive and negative real numbers are both possible for the dot product.
Cross Product
A Vector Product is a cross product. When two vectors of different types are multiplied together, it is called a cross product. In mathematics, a cross product or vector product is a consequence of multiplying two vectors and obtaining the product to be a vector quantity as well. It is perpendicular to the plane containing the two provided vectors, resulting in the final vector.
Vector Triple Product Definition
It is a subdivision of vector algebra in which the cross-product of three independent vectors is taken into consideration. To get the vector triple product, multiply the cross product of one vector by the cross products of the other two vectors and divide the result by three. The method produces a vector as a consequence of its execution. As a result of simplifying the vector triple product, the identity BAC – CAB identity, which is an abbreviation for BAC – CAB identity, is produced.
Vector triple product is an area of vector algebra that has a long history of research and publication in the discipline. When we look at a vector triple product, we may learn more about the cross-product of three vectors, which is quite useful.
Vector Triple Product Proof
In order to establish that the cross product is distributive over the subtraction of two vectors, there is a simple and straightforward method. Alternatively, the components of either vector may be negated to complete the operation. Because of this, the cross-product is more distributive than the sum of its parts.
Results of the triple product of vectors
The cross product of a vector with the cross products of the other two vectors may be used to calculate the triple product of that vector. A vector is generated as a result. The BAC – CAB identity may be found by simplifying the vector triple product.
Vector Triple Product Formula
The cosine of the angle between two vectors is used to compute the angle between the vectors. This formula is derived by taking the product of the two vectors’ separate components and dividing it by their product of magnitude. Formula for angle between the two vectors is shown below.
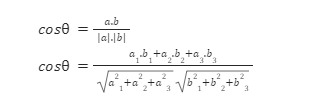
Conclusion:
The cross product of three vectors is the focus of the vector triple product branch of vector algebra. There is a way to calculate a vector’s triple product value by comparing its cross product with that of two other cross products. An output vector is generated by this method. The BAC – CAB identity is the result of simplifying the vector triple product.
 Profile
Profile Settings
Settings Refer your friends
Refer your friends Sign out
Sign out






