The ratios that are used in trigonometry are called sine, cosine, tangent, cotangent, cosecant, and secant (sec). Trigonometry, which is a subdivision of geometry, is an area of mathematics that deals with the sides and angles of triangles with right angles. Trigonometry is a subfield of geometry. As a result, the sides and angles of the triangle are considered while determining how to evaluate trig ratios.
The ratio of the lengths of the sides in a triangle with a right angle is used as the starting point for calculating the values of all of the trigonometric functions. The values of all of these ratios are what we mean when we talk about trigonometric ratios. The trigonometric ratios of a certain angle are found by comparing the lengths of the sides of a triangle with right angles to each other with respect to one of the triangle’s acute angles. This comparison is done in order to find the value of the angle.
The following are the three sides that make up a right triangle:
Hypotenuse (the longest side)
Perpendicular (opposite side to the angle)
Base (Adjacent side to the angle)
TRIGONOMETRIC RATIOS
Sine (sin), cosine (cos), tangent (tan), cotangent (cot), cosecant (cosec), and secant are the six trigonometric ratios. Sine (sin) is the opposite of cosine (cos) (sec). A subfield of geometry known as trigonometry, trigonometry is a discipline of mathematics that deals with the sides and angles of triangles with right angles. Therefore, trig ratios are evaluated in relation to the sides and angles of the triangle.
The following table presents the trigonometric ratios applicable to the angle denoted by ‘θ’:
Sin θ = Height/Hypotenuse
Cos θ = Base/Hypotenuse
Tan θ = Height/Base = sin θ/cos θ
Cot θ = Base/Height = 1/tan θ
Sec θ = Hypotenuse/Base = 1/cos θ
Cosec θ = Hypotenuse/Height = 1/sin θ
SOHCAHTOA: The lengths of the sides of a right triangle and SOHCAHTOA can be used to figure out what a trigonometric ratio is.
SOH stands for sin(θ), which means opposite/hypotenuse, CAH stands for cos(θ), which means adjacent/hypotenuse, and TOA stands for tan(θ), which means opposite/adjacent.
In the next two examples, we’ll use these steps, definitions, and equations to figure out how to use trigonometric ratios with right triangles that are similar to each other.
Example of Problem 1: Using Trigonometric Ratios with Similar Right Triangles
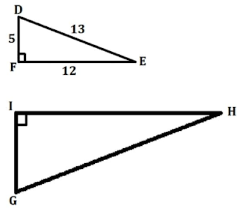
Both of the triangles below, DEF and GHI, are the same shape.
Use trigonometric ratios to figure out what sin(G) is.
Step 1: Find the sides and angles that match similar right triangles.
By finding the hypotenuse, shorter leg, and longer leg of each triangle, we can find the angles that go together:
Since DE and GH are both hypotenuses, they are the same.
Since FD and IG are both short legs, they are the same.
Since EF and HI are both the longer leg, they are the same.
Then, the angles that go with them are: ∠D and ∠G
∠E and ∠H
∠Fand ∠I
Step 2: Figure out which sides are needed for the ratio in trigonometry.
We need the side opposite G, which is HI, and the hypotenuse, GH, to find sin(G).
Step 3: Use the fact that the trigonometric ratios of similar triangles are the same to find the ratio you need for the triangle with all sides given.
Since the triangles are similar, the trigonometric ratios of the angles are the same. So we know that sin(G) = sin (D).
Using the opposite side and hypotenuse of D, which are also the opposite side and hypotenuse of G, we get:
sin(G)=sin(D)
=12/13
So, sin(G) equals 12/13.
Example Problem 2: Using Trigonometric Ratios with Right Triangles that are Similar
Both of the triangles below, ΔQRS and ΔTUV, are the same shape. Use trigonometric ratios to figure out what tan(U) is.
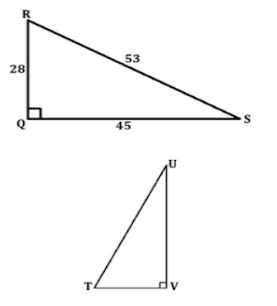
Step 1: Find the sides and angles of the similar right triangles that match up.
The sides that go together are:
TV and RQ
VU and QS
TU and RS
The angles that correspond to each other are as follows: ∠Q and ∠V
∠R and ∠T
∠S and ∠U
Step 2: Figure out which sides are needed for the ratio in trigonometry.
To find tan(U), we need the sides TV and VU, which are opposite and next to each other.
Step 3: Use the fact that the trigonometric ratios of similar triangles are the same to find the ratio you need for the triangle with all sides given.
We know that tan(U)=tan (S).
Using sides that go together, we have:
tan(U) = tan(S) =28/45
Therefore, tan(U) = 28/45.
Two triangles are similar
Two triangles are said to be similar to one another if their corresponding angles are congruent and the ratios of their respective sides are identical. Triangles that are similar yet have right angles (90 degrees) are called comparable right triangles. Triangles that are similar to one another have trigonometric ratios that are identical for matching angles.
Similar triangles Theorems Accompanied by Proofs
AA (or AAA) or Angle-Angle Similarity
If any two angles of one triangle are equal to any two angles of another triangle, then the first triangle and the second triangle are equivalent to one another and are therefore similar.
Based on the figure that was just presented to you, if ∠ A = ∠X and ∠C = ∠Z then ΔABC ~ΔXYZ.
As a direct consequence of the findings obtained, it is simple to deduce that
AB/XY = BC/YZ = AC/XZ
As a direct consequence of the findings obtained, it is simple to deduce that and ∠B = ∠Y
SAS or Side-Angle-Side Similarity
It is said that two triangles are similar to one another if the two sides of one triangle are in the same proportion as the two sides of another triangle, and if the angle inscribed by the two sides in both of the triangles is the same.
Therefore, given that∠A = ∠X and AB/XY = AC/XZ then ΔABC ~ΔXYZ.
From the congruency,
AB/XY = BC/YZ = AC/XZ
and ∠B = ∠Y and ∠C = ∠Z
SSS or Side-Side-Side Similarity
Similarity between two triangles can be determined by determining whether or not all three sides of one triangle are proportional to all three sides of the other triangle.
Therefore, since AB/XY = BC/YZ = AC/XZ then ΔABC ~ΔXYZ.
We can draw the following conclusions based on this result: ∠A = ∠X, ∠B = ∠Y and ∠C = ∠Z
Conclusion
Relationship Between Angles and Sides: In a triangle, the side that is opposite the angle that is the largest is also the side that is opposite the angle that is the smallest, and vice versa. The side that is opposing the angle that is the smallest is also opposite the side that is the largest. When we determine the ratio of two of a triangle’s sides, the ratio of the corresponding sides in every other triangle that has those same two sides will always be the same. As a result of this, it can be deduced that the trigonometric ratios (sine, cosine, and tangent) in triangles with comparable right angles are always equal to one another.
 Profile
Profile Settings
Settings Refer your friends
Refer your friends Sign out
Sign out