In real life Relation and Function give us the link between any two entities. In our day to day life, we come across many patterns and links that characterize relations such as a relation of a father and a son, brother and sister, etc. Hence, in Mathematics also, we come across so many relations between numbers such as a number x is more than y, line P is parallel to line Q, etc. Relation and function map are actually elements of one set (domain) to the elements of another set (codomain).
Functions are nothing but a very special types of relations that define the precise correspondence between one quantity with the other quantity. In this article, we will study or learn how to link different pairs of elements from two sets and then define or find out a relation between them, different types of relation and function, and the difference between relations and functions.
What are Relations and Functions?
Relations and functions actually define a mapping between two sets (Inputs and Outputs) such that they have ordered pairs of the form (Input, Output). Relation and function are very important concepts or parts in algebra. They are used very widely in Mathematics as well as in our day to day life. Let us define more clearly to each of these terms of relation and function to understand their meaning.
Relation and Function Definition
Relation and function can be individually defined as follows:
- Relations – A relation R from a non-empty set B is a subset of the cartesian product A × B. The subset is actually derived by describing a relationship between the first element and the second element of the ordered pairs in A × B.
- Functions – A relation f from a set A to a set B is mainly said to be a function if each and every element of set A has one and only one image in set B. In other words, we can also say that no two distinct elements of B have the same pre-image.
Kindly note that all functions are relations but all relations are not functions.
Representation of Relation and Function
Relations and functions can be represented in so many different forms such as arrow representation, algebraic form, set-builder form, graphically, roster form, and tabular form. Define a function f: A = {1, 2, 3} → B = {1, 4, 9} such that f(1) = 1, f(2) = 4, f(3) = 9. Now, let us represent these functions in many different forms.
- Set-builder form – {(x, y): f(x) = y2, x ∈ A, y ∈ B}
- Roster form – {(1, 1), (2, 4), (3, 9)}
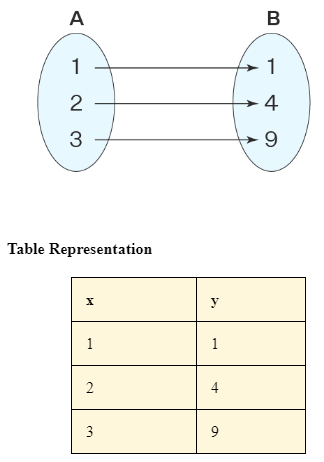
Terms Related to Relation and Function
From the above discussion we have already understood the meaning of relation and function, let us understand the meanings of a some more terms related to relations and functions that will help us to understand the concept very clearly or we can say that in more better way.
Cartesian Product – Given two non-empty sets P and Q, the cartesian product P × Q is actually the set of all ordered pairs of elements from P and Q, that is, P × Q = {(p, q): p ∈ P, q ∈ Q}
Domain – This is the set of all first elements of the ordered pairs in a relation R from a set A to a set B is called the domain of the relation R. It is called the set of inputs as well as pre-images.
Range – This is the set of all second elements of the ordered pairs in a relation R from a set A to a set B is called the range of the relation R. It is called the set of outputs as well as images.
Codomain – This is the whole set B in a relation R from a set A to a set B is called the codomain of the relation R. Range ⊆ Codomain.
Types of Relation and Function
There are many or different types of relations and functions that have very specific properties which make them different and unique. Let us study the list of types of relations and functions given below:
Types of Relations
The different types of relations are given below:
Empty Relation – A relation is said to be an empty relation, if it has no elements, that is, no element of set A is mapped or linked to any element of A. It is denoted by R = ∅.
Universal Relation – A relation R in a set A is actually a universal relation if each element of A is related to every element of A, i.e., R = A × A. It is called the full relation.
Identity Relation – A relation R on A is said to be an identity relation if each and every element of A is related to itself, that is, R = {(a, a): for all a ∈ A}
Inverse Relation – Define R to be a relation from set P to set Q i.e., R ∈ P × Q. The relation R-1 is said to be an Inverse relation when R-1 from set Q to P is denoted by R-1 = {(q, p): (p, q) ∈ R}.
Reflexive Relation – A binary relation R given on a set A is said to be reflexive if, for every element a ∈ A, we have aRa, that is, (a, a) ∈ R.
Symmetric Relation – A binary relation R defined on a set A is generally said to be symmetric if and only if, for elements a, b ∈ A, we have aRb, that is, (a, b) ∈ R, then we have bRa, that is, (b, a) ∈ R.
Transitive Relation – A relation R is said to be transitive if and only if (a, b) ∈ R and (b, c) ∈ R ⇒ (a, c) ∈ R for a, b, c ∈ A
Equivalence Relation – A relation R showed on a set A is said to be an equivalence relation if and only if it is reflexive, symmetric and transitive.
Types of Functions
Here, I am giving different types of functions, lets have a look –
One-to-One Function – A function f: A → B is generally said to be one-to-one function, if each element of A is mapped to a distinct element of B. we say it Injective Function also.
Onto Function – A function f: A → B is said to be onto function, if each and every element of B is the image of some element of A under f, here it is very clear that., for every b ∈ B, there is an element exist in A such that f(a) = b. A function is onto if the range of the function = B.
Many to One Function – A many to one function is defined by the function f: A → B, when more than one element of the set A is connected to the same element which are actually given in the set B.
Bijective Function – A function is bijective if it has both one-to-one and onto function.
Constant Function – The constant function is of the form f(x) = K, where K is actually a real number. For the different types of values given of the domain (x value), the same range value of K is obtained for a constant function.
Identity Function – An identity function is a function where each and every element in a set B gives the image of itself as the same element i.e., g (b) = b ∀ b ∈ B. Hence, we can say that, it is of the form g(x) = x.
Conclusion
If we think of the relationship between two quantities, we can also think of this relationship in terms of an input/output machine. If there is only one and only one output for every input, we have a function. Hence, we can conclude that the given set of pairs does not represent any function. It is actually a relation.
Consider another example,
- F (x) = 3x +2 and g(x) = 5x -1. If h(x) = fg(x) , find value of h(2)
G (2) = 5(2) -1
= 10-1
= 9
Now this output will serve as input
F (9) = 3(9) +2 = 29
H (2) = 29
- Find (g ∘ f) (x) if, f(x) = 6 x² and g(x) = 14x + 4
Substitute x in g(x) = 14x + 4 with 6 x²
⟹g [f(x)] =14 (6 x²) + 4
= 84 x² + 4
- For f(x) = 3x + 4 and g(x) = 5, find (f ◦ g) and (g ◦ f).
Solutions: (f ◦ g) (x) = f(g(x)) = f (5) = 3(5) + 4 = 19
(g ◦ f) = 5 itself.
Conclusion
Algebraic operations can be performed on functions. When functions are combined the output of the inner function becomes the input of the outer function. The domain of a composite function consists of those inputs in the domain of the inner function which correspond to the outputs of the inner function that are in the domain of the outer function. Just as we combine functions to form a composite function, we can decompose composite functions into simpler functions too.
 Profile
Profile Settings
Settings Refer your friends
Refer your friends Sign out
Sign out






