Profile
Settings
Refer your friends
Sign out
It has been found that the focal length of a spherical mirror, whether it is concave or convex, is equal to half of its radius of curvature. However, both concave and convex mirrors have the same relationship between focal length and radius of curvature.
In addition, the radius of the hollow sphere of which the spherical mirror is a part is called the radius of curvature of the spherical mirror. In other words, one can also say that the distance between the pole and the centre of curvature of the spherical mirror is called its radius of curvature. It is denoted by R. Additionally, the distance between the pole and focus is the focal length represented by f.
Focal Length and Radius of Curvature
If a beam of light falls on the principal axis of a concave mirror, all the rays meet at a specific point. Thus, that particular point is called focus or Focal Point on the concave mirror. However, if all the light is reflected and we try to join the actual path of the ray in front of the mirror, that point is called the focus. In addition, the straight line passing through the pole of the spherical mirror and the centre of curvature of that line is called the principal axis of the spherical mirror. It is usually denoted by P. The focal length is the distance between the principal axis and the focus or focus point.
The radius of curvature is half of the principal axis. However, one can also say the radius of the hollow sphere of which the spherical mirror is a part is called the radius of curvature of the spherical mirror.
Some Spherical Mirror Related Terms
There are some terms that you should know before proving the relationship between the focal length and the radius of curvature. However, they are:
- Aperture
- Pole
- Centre of curvature
- Radius of curvature
- Principal axis
- Focus
- Focal length
- Focal Plane
- Real Image
- Virtual Image
Relationship between the Focal Length and the Radius of Curvature
If we talk about the relationship between the focal length and the radius of curvature, the formula is:-
Focal length = Radius of curvature/2
Or
f = R/2
Proving relationship between the focal length and the radius of curvature:
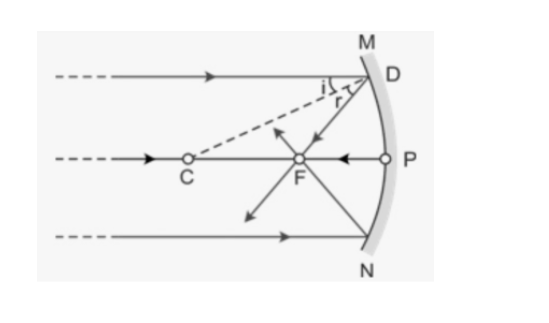
In the diagram given above, M and N represent the spherical mirror. However, P is the principal axis, C is the centre of curvature, F is the focal point where the two rays meet each other. In addition, the distance between the C and P is called the radius of curvature, and the distance between F and P is called the focal length.
The ray of light incident on the mirror is parallel to the principal axis. The ray of light AB generally strikes on the surface. CP is equal to R (radius of curvature ). However, when the two parallel rays A and B strike on the mirror, they reflect and pass through the focus point. As the law of reflection is followed, i = r,
According to the figure of the geometry,
∠BPC = θ = i
In D CBF, θ = r
BF = FC (according to the law of reflection i = r)
When the mirror’s aperture is smaller than, B lies near to P, and therefore, the condition becomes BF = PF.
FC = FP = Pf,
PC = PF + FC = PF + PF
R = 2 PF = 2f
So, f = R/2
Thus, this relationship is also applicable for convex mirrors. According to the derivation, the radius of curvature is equal to the toys of focal length in a spherical mirror. Hence we can say that R = 2f.
Conclusion
The radius of curvature is twice the focal length, or focal length is half of the radius of curvature. However, both conditions are the same. In addition, both the concave and convex mirrors experienced the exact relationship between the focal length and the radius of curvature.
In conclusion, you must have to clear your concept related to principles, formation of image of spherical mirror, concave and convex mirror.
