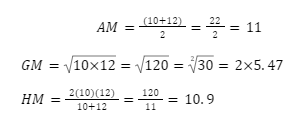Relation Between AP,GP and HP

AP,GP and HP represents the series’ average or mean. The letters AM, GM, and HM stand for Arithmetic Mean, Geometric Mean, and Harmonic Mean, respectively. Arithmetic Progression (AP), Geometric Progression (GP), and Harmonic Progression (HP) mean AM, GM, and HM, respectively.

The value of AM is greater than the value of GM and HM, which explains the relationship between AM, GM, and HM. The geometric mean is bigger than the harmonic mean for a given set of data points. The following expression represents the relationship between AM, GM, and HM: AM > GM > HM.

The AM GM HM relationship is important for better understanding the arithmetic mean (AM), geometric mean (GM), and harmonic mean (HM) (HM). The product of the arithmetic and harmonic means equals the square of the geometric mean.

AM, GM, and HM

Arithmetic Mean (AM): The basic average or mean of a group of numbers is known as the AM. The total of all the numbers in the series is divided by the number of numbers in the series.

Geometric Mean (GM): When compounding, the geometric mean (GM) is applied. It’s the nth root of the sum of the series’ numbers.

Harmonic Mean (HM): The harmonic mean (HM) is the reciprocal of the mean of the numbers in the series.

AP, GP and HP Relation

Arithmetic, Geometric, and Harmonic Means, to be precise. AM, GM, and HM are represented by Arithmetic Progression (AP), Geometric Progression (GP), and Harmonic Progression (HP), respectively.

Assume that a and b are both real numbers.

The arithmetic mean(AM), geometric mean(GM), and harmonic mean(HP) formulas are as follows for any two numbers a, b. The arithmetic mean, commonly known as the average of the provided numbers, is equal to the sum of the two numbers divided by two for two numbers a, b.

Between two numbers a and b, the arithmetic mean is AM= a + b / 2

The square roots of the product of the two numbers a, b are equal to the geometric mean of the two numbers. Furthermore, if there are n data points, the geometric mean is equal to the nth root of the n numbers’ product.

 Between a and b, the geometric mean is GM= √ ab

1/a represents the harmonic mean of two numbers. The inverse of their arithmetic mean is equal to 1/b. The harmonic mean of these two numbers is equal to (a + b)/2ab, which is the inverse of the arithmetic mean.

Between two numbers a and b, the harmonic mean is HM=2ab / a + b

AP, GP and HP Relation Formula

The product of arithmetic mean and harmonic mean equals the square of the geometric mean is the formula describing the relationship between AM, GM, and HM. This can be expressed as this expression.

The formula for the relationship between AM, GM, and HM is:

GM= √AM+HM

If the harmonic mean HM between a and c is HP, then

b=2ac / a + c

If the AM, GM, and HM of two separate positive numbers are A, G, and H, then

A>G>H 

A, G and H are in GP

G²=A×H or G²=AH

AP, GP and HP Examples

AP, GP, HP examples are given below:

Find the link between AM, GM, and HM for the two data points 10, 12, and arrange them in ascending order.

The data points are 10, 12 

As a result, we have AM>GM>HM

Conclusion

In this article we will conclude that, The relationship between AM, GM, and HM aids in the comprehension of a progression or mathematical series. Arithmetic mean (AM), Geometric mean (GM), and Harmonic mean (HM) are the three types of mean. They are all mathematical series that are utilized in sequence and series, which may be defined as a collection of objects that are ordered in a particular order. In mathematics, we have three popular sequences: Arithmetic Sequence, Geometric Sequence, and Harmonic Sequence. Each one has a different meaning and, as a result, diverse applications.