Rolle’s theorem says that if a differentiable (real-valued) function has equal values at two different places, it must have at least one fixed point between them, that is, a position where the first derivative (the slope of the tangent line to the function graph) is zero. Michel Rolle, a French mathematician, is the name of the theorem. The mean value theorem is a specific case of Rolle’s Theorem.

The mean value theorem of Lagrange is sometimes known as the first mean value theorem or the mean value theorem. The mean is commonly thought of as the average of the supplied values, however, the procedure for obtaining the mean value of two independent functions in integrals is different. In this article, we will prove the rolle’s theorem and its related conditions.

Mathematical Statement of Rolle’s Theorem

If a function f is defined in the closed interval [a, b] such that it meets the following requirements: 

1. The function f is continuous on the closed interval [a, b],
2.  The function f is differentiable on the open interval (a, b), and
3.  If f (a) = f (b), then there exists at least one value of x, which is between a and b, i.e. (a c b), in such a way that f'(c) = 0. If a function is continuous on the closed interval [a, b] and differentiable on the open interval (a, b), then f'(c) = 0.

Rolle’s theorem can be expressed mathematically as follows: Let f: [a, b] R be continuous on [a, b] and differentiable on (a, b), such that f(a) = f(b), where a and b are real numbers. Then some c in (a, b) exists such that f′(c) = 0.

Proof of Rolle’s Theorem

When directly proving a theorem, you begin by assuming that all of the requirements are met. As a result, the following explanation is limited to functions that are differentiable, continuous, and have f(a) = f (b).

Keep in mind that when a function obeys Rolle’s Theorem, the point where f′(x)=0 happens at a maximum or minimum value (i.e., extrema).

How can we know if a function will have one of these extrema in the first place? The Extreme Value Theorem states that if a function is continuous, it will always have both a maximum and a minimum point in the interval. For our function, we now have two fundamental options.

Case 1: The function is constant 

Case 2: The function is variable.

Let’s take a closer look at each of these scenarios.

The function is constant in case 1

The graph of a constant function is a horizontal line segment.

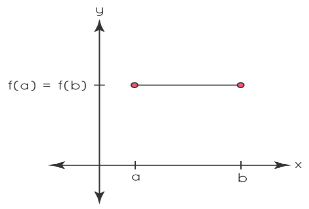
Because the derivative is zero everywhere, every point, in this case, satisfies Rolle’s Theorem. (Recall that Rolle’s Theorem ensures at least one point.) Multiple points are not excluded!

Case 2: The function is variable.

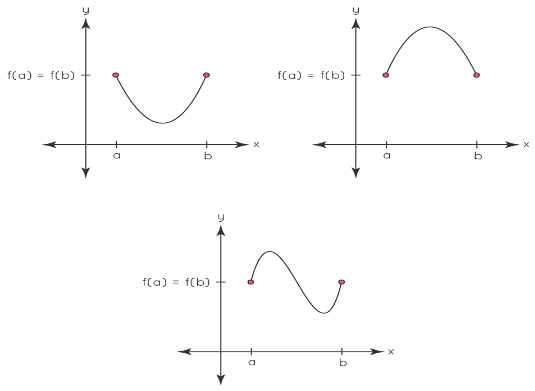
The function must change directions to start and end at the same y-value because it isn’t constant. This means the function will have a minimum (left graph), a maximum (middle graph), or both somewhere inside the interval (right-hand graph).

Now we must show that the derivative must equal zero at this inner extrema. The remainder of this discussion will concentrate on scenarios in which the interior extrema is a maximum, but the reasoning for a minimum is substantially the same.

Possibility 1: Is it possible that the maximum will occur when f′>0?

No, because we know the function is rising when f′>0. It cannot, however, increase because we have reached the limit.

Possibility 2: Is it possible that the maximum will occur at f′0?

No, because if f′0 is decreasing, we know that function was greater just a little to the left of where we are now. It couldn’t have been larger because we’re at the function’s maximum value. Because f′ exists but is neither larger nor smaller than zero, the only remaining choice is that f′=0. That’s everything! We demonstrated that the function must have extrema, and that the derivative must equal zero at the extrema!

Example on Rolle’s Theorem

Verify Rolle’s theorem for the functions y = x2 + 2, a = –2, and b = 2

The function y = x² + 2 is continuous in [– 2, 2] and differentiable in (– 2, 2), according to Rolle’s theorem formulation.

Given the circumstances,

f(x) = x² + 2

f(-2) = (-2)² + 2 = 4 + 2 = 6

f(2) = (2)² + 2 = 4 + 2= 6

Thus, f(– 2) = f(2) = 6

As a result, the function f(x) is continuous in the range [-2, 2].

Now, f'(x) = 2x

According to Rolle’s theorem, there is a point c (– 2, 2) where f′(c) = 0.

f′(c) = 2(0) = 0 at c = 0, when c = 0 (− 2, 2)

As a result, Rolle’s theorem is proven.

Conclusion

Under the conditions: f (x) be a continuous function on the interval [a, b] and differentiable on the open interval (a, b), there exists at least one value c of x such that f'(c) = [f (b) – f (a)] / (b – a).