Properties of Conjugate

The complex conjugate of any given complex number is another complex number that is connected with that particular complex number. A complex conjugate of a complex number is another complex number that has the same real part as the first complex number, but the imaginary part has the same magnitude but the opposite sign. This second complex number is called a complex conjugate of the first complex number. A real number is created when a complex number and its complex conjugate are multiplied together.

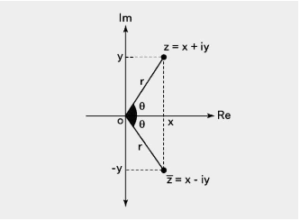
The complex conjugate of a complex number is the number that gives the mirror image of the complex number about the real axis in the Argand plane. 

Conjugate Complex: 

A second complex number is said to be a complex number’s complex conjugate if the real part of the second complex number is the same as the real part of the first complex number, and the magnitude of the second complex number’s imaginary part is the same but with the opposite sign. A complex number has the form a + ib, where a and b are both real numbers, a is considered to be the real portion of the number, b is considered to be the imaginary component of the number, and i is an imaginary number that is equal to the root of -1. The conjugate of the complex expression a + ib, whose real portion is a and whose imaginary component is b, is given by the expression a – ib, whose real part is a and whose imaginary part is b. The reflection of a+ib about the real axis (X-axis) in the argand plane is denoted by the expression a-ib. When trying to justify a complex number, it is helpful to look at the complex conjugate of the number in question. 

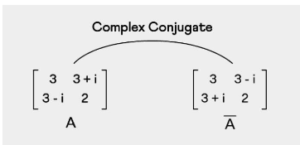
Complex Conjugate of a Matrix: 

A matrix A with complex elements has a complex conjugate if there is another matrix whose entries are the complex conjugates of the entries in matrix A. Consider the row matrix A = [1-i    4+2i    3+7i], where each entry in matrix B is the conjugate of each entry in matrix A. The complex conjugate of matrix A is denoted by the expression B = [1+i    4-2i    3-7i]. The symbol A is used to represent the complex conjugate of the matrix A. Let’s take a look at one more example of a matrix that has complex entries, and then figure out what its complex conjugate is.

Complex Conjugate root Theorem: 

According to the complex conjugate root theorem, if f(x) is a polynomial with real coefficients and a + ib is one of its roots, where a and b are real numbers, then the complex conjugate of a – ib is also a root of the polynomial f, and this is true even if a and b are not real numbers.

Let’s look at a concrete illustration of a polynomial that has complex roots so that we may get a better grasp of the theory. Consider f(x) = x³ – 7x² + 41x – 87. The roots of the polynomial f(x) are now revealed to be the numbers 3, 2 + 5i, and 2 – 5i. Here, the roots of f(x) are shown to be 2 + 5i and 2 – 5i, which are conjugates of one another. It follows from this that non-real roots, also known as the complex roots of a polynomial, are always found in pairs. If we already know the value of one complex root of a polynomial, then we don’t need to perform the calculation to determine whether or not the complex conjugate of that root is also a root of the polynomial.

Properties of Complex Conjugate: 

Now that we have everything out of the way, let’s talk about a few aspects of complex conjugate that can make our computations simpler and less difficult. Take into consideration the complex conjugates of two numbers, z and w, which are denoted by the symbols z and w, respectively.

• The complex conjugate of the product of two complex numbers is equal to the product of the complex conjugates of the two complex numbers.
• The complex conjugate of the quotient of two complex numbers is equal to the quotient of the complex conjugates of the two complex numbers.
• The complex conjugate of the sum of two complex numbers is equal to the sum of the complex conjugates of the two complex numbers.
• The complex conjugate of the difference between two complex numbers is equal to the difference between their complex conjugates.
• The difference between a complex number and its complex conjugate is equal to twice the imaginary part of the complex number. 

Conclusion: 

The complex conjugate is applied when rationalising complex numbers and determining the amplitude of a complex number’s polar form, both of which require the complex number to be represented. Finding the probability in quantum mechanics is one use of the complex conjugate that may be found in the field of physics.