Properties of a Triangle

The sides and angles of a triangle must follow certain rules to construct a triangle of accurate measure. And that is why there is a need to understand the mandatory conditions that apply to the sides and angles of a triangle. Once we are acquainted with these properties, it will help us in figuring out the solution to that triangle to a great extent. These properties in themselves give an account of the characteristics that are related to a triangle. 

Sum of all the Angles of a Triangle

Sum of Internal Angles

Let there be a line segment of length ‘l’. Now, take three points on that line segment and bend over those three points to form an enclosed figure. That figure will be a triangle.

Now, it is known that a straight line represents an angle of 180°. Therefore, a figure that is made up of that same segment will also give the total of that same angle. Hence, it can be stated that the sum of all internal angles of a triangle is 180°. 

Sum of Exterior Angles

Similarly, it can also be proven that the sum of exterior angles of a triangle is 360°. 

The angle around a point is 360°. A triangle is made up of three such points. Therefore, the sum of all those angles will conclude to be (360° + 360° + 360° =) 1080°. 

Now, as the interior and exterior angles of a triangle are supplementary, the measure of this total angle will be reduced to its half. And the angle will remain to be (1080° – 540° =) 540°.

Finally, subtracting the sum of interior angles of the triangle from this sum, we will get the sum of exterior angles of that triangle. 

540° – 180° = 360°

Hence, it can be concluded that the sum of exterior angles of a triangle is 360°.

The Sum of the Length of the two Sides of a Triangle

This happens to be one of the foremost conditions for a triangle that the sum of the length of any two sides of a triangle must always exceed the length of the third side. If this condition for a triangle is not satisfied, then either the triangle will not be of appropriate measure, or no triangle will be formed as a result at all.

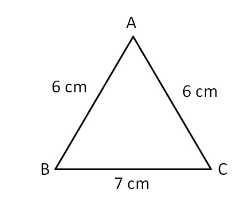
Take this figure, for example, the sum of any two sides of this triangle will always be greater than the third side.

AB = 6cm

BC = 7cm

CA = 6cm

AB + BC > CA

BC + CA > AB

AB + CA > BC

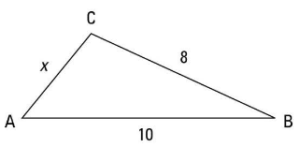
Now, taking this figure for example, 

It can easily be stated that the side AC for this triangle will be less than 18 units.

This condition stands true for all types of triangles, equilateral, scalene, obtuse, acute, right-angled, or obtuse. Every triangle has to follow this rule to form a figure of accurate measure. 

Else, think of a triangle in which the three sides are 3cm, 6cm, and 9cm. Now, it is not possible to make a triangle of this exact measure with these lengths. The reason for it is that the sum property of the triangle is not satisfied. The 9cm length of the triangle will not meet ends with the end of the other two sides.

Equal to 180°

Following are some of the properties of a triangle that are related to the angles of a triangle:

• The hypotenuse of a right-angled triangle happens to be the longest side of that particular triangle.

It can easily be proved by the means that the angle that is opposite to the hypotenuse of that triangle will be 90°, and that angle will be the largest one in that angle.

• Perpendicular to any side of the triangle from any particular vertex gives the height of that triangle.

The side over which the perpendicular falls is referred to as the base, and the perpendicular itself represents the height of the triangle.

• If two angles of a triangle are of the same measure, then the sides opposite to those angles will also be equal.

This property of the angles can also be observed in isosceles triangles. Two sides of that triangle are the same, and the angles opposite to those sides are of the same degree measure too.

• The sum of internal angles of a triangle is 180°. 

The measure of exterior angle can also be found if we know the angles inside the triangle other than the one adjacent to the external angle.

Conclusion

The angles and the sides that constitute themselves to form a triangle have their own set of properties. Like, the sum of their inside angles will always be 180°. This set of rules is meant to be followed, or the construction of that specific triangle will not be completely accurate. Therefore, to get a better understanding of this topic, study of such topics is much deserved. This is how we get to know about the limits within which the measures of that triangle lie.