Problems with De Moivre’s identity

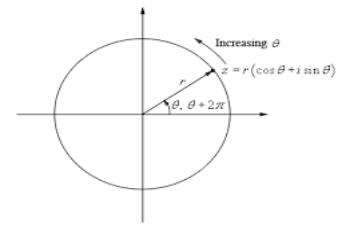
De Moivre’s identity: If z = rcosθ+isinθ

Now, if we want to compute zn, where n is any rational number, then we have-

Zn = (rcosθ + isinθ)n

So, according to DeMoivre’s identity, we have 

Zn = rn(cosnθ + isin(nθ))

DeMoivre’s HOTS Questions

Now, we can use DeMoivre’s identity in various forms and develop our high-order thinking skills so we can use this identity on an advanced level.

We will concentrate on various forms of this theorem by trigonometric correlation and trigonometric formulas/relations.

For example:

1. (cosθ + isinθ)-n =cos(-nθ) + isin(-nθ)

=cosnθ – isin(nθ)

1. (cosθ – isinθ)n =cosnθ – isin(nθ)
2. (cosθ – isinθ)-n =cos(nθ) + isin(nθ)

Note: cos(-θ) =cosθ

sin(-θ)=sinθ

Now, we can also represent an equation in polar form into its Euler form which is given by :

eiθ =  cosθ + isinθ

e-iθ = cos(-θ) + isin(-θ)

e-iθ =  cosθ – isinθ

Now we have-

eiθ + e-iθ = cosθ + isinθ + cosθ – isinθ = 2cosθ

eiθ – e-iθ = cosθ + isinθ – cosθ + isinθ = 2isinθ

These two equations are very important in solving higher-level questions (HOTS) based on this topic.

If eia = cosa + isina and eib = cosb + isinb

Then eia * eib = e(ia+ib) = ei(a+b)

which will give us ei(a + b) = cos(a +b) + isin(a +b).

So we have: (cosa + isina).(cosb + isinb) = cos(a + b) + isin(a + b) ………… (I)

This equation is used to simplify many HOTS when the multiplication of complex numbers is involved.

• Problem (HOTS) based on DeMoivre’s Theorem

Here, we will focus on different types of problem sets that are developed on DeMoivre’s Theorem.

A- Proof z = (√3/2 + i/2)5 + (√3/2 – i/2)5 = 2cos(150°)

Here, we have to put √3/2 = rcosθ and 1/2 = rsinθ

Now, we have (rcosθ)2 + (rsinθ)2 = 3/4 + 1/4 = 1.

so  r2(cos2θ + sin2θ) = 1 

hence, r2 = 1 ⇒ r =1

Now rsinθ = 1/2 ⇒ sinθ = 1/2

⇒ θ = 30°

Now z = (cosθ + isinθ)5 + (cosθ – isinθ)5

= cos5θ + isin5θ + cos5θ – isin5θ

=2cos5θ ⇒ 2cos150°           

B- If cos α + cosβ + cosγ  = sinα +sinβ +sinγ = 0 then prove that:

cos3α + cos3β +cos3γ = 3cos(α+β+γ)

Now, we take sinα + sinβ + sinγ = 0, multiply both sides with i and then add it to cosα + cosβ + cosγ

So we have i(sinα + sinβ +sinγ) + (cosα + cosβ + cosγ) = 0

= cosα + isinα +cosβ + isinβ + cosγ + isinγ = 0

Now let z1 = cosα + isinα

z2 = cosβ + isinβ

z3 = cosγ + isinγ

and we have z1 +z2 +z3 = 0

Through algebra, we know that z13 + z23 + z33 – 3z1.z2.z3 = (z1 + z2 + z3).(z12 + z22 + z32 – z1z2 – z2z3 – z3z1)

so z13 + z23 + z33 = 3z1z2z3

Now, we have (cosα + isinα) 3 + (cosβ + isinβ)3 + (cosγ + isinγ)3

= 3(cosα + isinα)(cosβ + isinβ)(cosγ + isinγ)

⇒ (cos3α + isin3α) + (cos3β + isin3β) + (cos3γ + isinγ3γ)

= 3[cos(α+β +γ) + isin(α+β +γ)]  from (i)         {see theory part}

Now, equate real part to real part, then we have

cos3α + cos3β + cos3γ = 3cos(α+β +γ)

Conclusion

Evaluation of problems based on the power of complex numbers can become hectic if we start multiplying the complex number by itself for n number of times. In this type of situation, DeMoivre’s Identity states that if Zn = (rcosθ + isinθ)n, then

Zn = rn(cosnθ + isinn(θ)) is useful.

DeMoivre’s Identity is applied in the polar form of a complex number and can help us interrelate complex numbers and trigonometric functions. It can be further used by converting the polar form of complex numbers into its Euler form, which can further simplify the problems (HOTS) based on this identity.