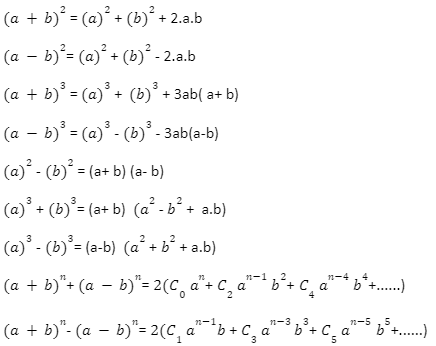Problems on Binomial Theorem

The binomial theorem is an algebraic formula by which we can find the value of any positive integer exponent of a binomial of the form x y as a polynomial of the nth degree of x and y. When a binomial is in the greater form, then only the multiples of the term are the binomial factors. We already know how to find the square and cube of terms like a+ b and a – b. Sometimes it happens that some terms come in which there is a coefficient of 6 or 7 or more. In this case solving it becomes complicated. Then the binomial theorem comes in handy. The binomial theorem gives us a simple way to simplify such large terms.

History of binomial theorem

Since the 4th century BC, humankind has been able to demonstrate the binomial theorem. This cube binomial was also utilised in the 6th century AD. Halyudh, an Indian mathematician, established this approach in the 10th century AD utilising Pascal’s triangle. In the 12th century, this theorem was explicitly established. Mathematicians advanced these findings until Sir Isaac Newton, in 1665, expanded the binomial theorem to all exponents.

Binomial theorem formula

As we read above, the Binomial Theorem tells us how to easily solve binomials with large exponents. Its formula is also similar. We just have to put the values ​​in it and after that we have to calculate. Because (a+b)n  is a binomial, and a + b is the binomial, the expansion of (a+b)n may be simply determined using the binomial theorem. But first, let’s get a rudimentary understanding of the binomial theorem. We’ll learn how to calculate the binomial expansion formula here.This solves the binomial with the largest exponent. Its formula is as follows:

What is K in the binomial theorem?

It is the symbol for a binomial coefficient. The upper index n is the exponent of the expansion; the lower index k indicates which term begins with k = 0. For example, when n = 5, in the expansion of each term

What is the binomial series, and how does it work?

The Maclaurin series, commonly known as the binomial series, is a unique series in mathematics. This series is a variant of the binomial theorem, with a=1 and b=x. The series can be converging or diverging depending on the values of a and n.

When implementing the Binomial Theorem, there are a few considerations to keep in mind. These are the following:

• From n to zero, the exponents of the first term (a) fall.
• The second term’s exponents increase from zero to n.
• The product of a and b’s exponents equals n.
• The first and last terms’ coefficients are both 1.
• To comprehend the Binomial Theorem in practice, let’s apply it to several phrases.

Binomial theorem expression

A binomial expression in algebra is made up of two terms connected by an addition or subtraction sign. Binomial expressions include (a+ b) and (6 – b), for example. We may need to enlarge binomial expressions on occasion, as demonstrated below.

Conclusion

In statistical and probability analysis, the binomial theorem is frequently employed. It is quite beneficial, as our economy is heavily reliant on statistical and probability analysis. The binomial theorem is used in advanced mathematics and calculating to determine the roots of equations in higher powers.