Profile
Settings
Refer your friends
Sign out
Permutation and combination is a topic of mathematics which helps you to arrange or select different objects or people or anything out of a given number of objects or things without actually listing them. Use some basic counting techniques to determine the number of different ways of arrangement of objects we can use. Basically we have two techniques, one is multiplication and the other one is addition. If we have two events say A and B. And say ‘m’ is the number of ways in which an event A can occur associated with each way of occurring of A another number B can occur in ‘n’ different ways. Then the total number of occurrence of the two events in the given order is m * n.
But if we have an event A which can occur in ‘m’ ways and another event B which can occur in ‘n’ ways and suppose both cannot occur together which mean we have to choose a or b then, they can occur in m+ n ways.
Permutation
Permutation is the arrangement of objects or person taking one or more at a time from the total objects. Permutations can be calculated with or without repetitions. Let r = different objects and n = total objects, then permutation is given by:
Combination
The ways of selecting or choosing different person or object out of the total objects are person taking one or more than one at a time is called combination. Let r = different objects, n= total objects.
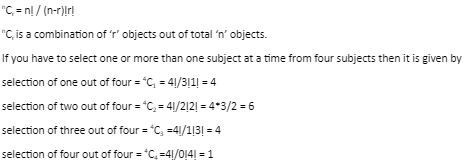
Formula
Factorial
The factorial function of a number is a natural number with a factorial sign. Factorial of a number is denoted by Ị
For example: 4Ị = 4*3*2*1 i.e. Reduce 1 from the given number and multiply the number till we reach 1 at last.
Conclusion
In this article you have studied about permutation & combinations. Permutation relates to the arrangement of all the members of a set into some position or order. Combination is the way of selecting items in which the order or sequence of selection doesn’t matter. Formula to calculate permutation is
means Multiply 6 in decreasing order until you get 1 i.e.6*5*4*3*2*1. We use permutation when we have to we have to arrange the objects and different orders are to be counted. Use combination if a problem is for the number of ways of selecting objects and the Order of selection is not important.
