A partial differential equation in mathematics is an equation that imposes relationships between the various partial derivatives of a multivariable function.
The function is frequently referred to as an “unknown” that must be solved for, in the same way that x is referred to as an “unknown” number that must be solved for in an algebraic equation such as x2 – 3x + 2 = 0. For partial differential equations, it is, on the other hand, almost always impossible to write down explicit formulas for their solutions. As a result, there is a tremendous amount of current mathematical and scientific research into methods for numerically approximating solutions of certain partial differential equations using computers in modern mathematics and science. Partial differential equations also occupy a significant portion of pure mathematical research, where the most frequently asked questions concern the identification of general qualitative characteristics of solutions to a variety of partial differential equations, in general.
Partial differential equations are common in mathematically oriented scientific fields such as physics and engineering, and they are also common in mathematics. To name a few examples, they are essential to modern scientific understanding of such phenomena as sound, heat diffusion, electrostatics, electrodynamics, thermodynamics, fluid dynamics, elasticity, General Relativity, and quantum mechanics (Schrodinger equation, Pauli equation, etc). Theorems of differential geometry and the calculus of variations, among other applications, are derived from many purely mathematical considerations.
Ordinary differential equations are a subclass of partial differential equations that correspond to functions of a single variable. Ordinary differential equations are also known as single variable differential equations. As of 2020, stochastic partial differential equations and nonlocal equations are two of the most widely studied extensions of the concept of partial differential equations. PDEs of the elliptic and parabolic types, as well as fluid mechanics, Boltzmann equations, and dispersive partial differential equations, are some of the more classical topics that are still the subject of much active research.
Partial differential equation classification:
There are certain functionalities that are present in each type of PDE that aid in determining whether a particular finite element approach is appropriate for the problem being described by the PDE or not. Several variables contain partial derivatives with respect to the variables, and the solution is dependent on the equation and variables. In mechanics, there are three different types of second-order partial differential equations. They are,
PDE with elliptic curves
PDE (parabolic differential equation)
PDE with a hyperbolic slope
Take the following example: auxx+buyy+cuyy=0, u=u (x,y). A given point (x,y) is said to be Elliptic when the equation b2-ac<0 ; this is a property that is used to describe the equations of elasticity without including the term “inertia.” If the condition b2-ac>0 is satisfied, hyperbolic PDEs can be used to describe the phenomenon of wave propagation. It should satisfy the condition b2-ac=0 in the case of parabolic PDEs. The heat conduction equation is an example of a parabolic partial differential equation (PDE).
Partial differential equation types:
The following are the different types of partial differential equations:
First-order partial differential equation: When we talk about the first-order partial differential equation in mathematics, we are referring to the equation that contains only the first derivative of the unknown function with variables. It is shown as below:
F(x1,…,xm, u,ux1,…,uxm)= 0
Quasi-Linear partial differential equation: An equation is said to be quasi-linear if all of the terms that have the highest order derivatives of dependent variables occur linearly, which means that the coefficients for all of those terms are only functions of the dependent variables’ lower-order derivatives. Terms with lower-order derivatives, on the other hand, can appear in any order.
Homogeneous partial differential equation: If all of the terms of a partial differential equation contain the dependent variable or its partial derivatives, the PDE is referred to as a non-homogeneous partial differential equation; otherwise, it is referred to as a homogeneous partial differential equation.
Partial differential equation example:
The following are some examples of second-order PDE:
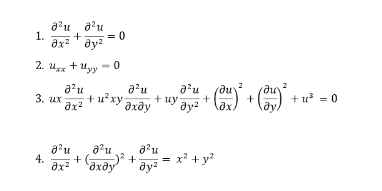
Conclusion:
PDEs are mathematical equations that involve two or more independent variables, an unknown function (that is dependent on those variables), and partial derivatives of the unknown function with respect to the independent variables.Partial differential equations are common in mathematically oriented scientific fields such as physics and engineering, and they are also common in mathematics.Theorems of differential geometry and the calculus of variations, among other applications, are derived from many purely mathematical considerations.
Ordinary differential equations are a subclass of partial differential equations that correspond to functions of a single variable. Ordinary differential equations are also known as single variable differential equations.
 Profile
Profile Settings
Settings Refer your friends
Refer your friends Sign out
Sign out






