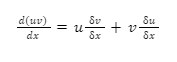The partial derivative of a function of several variables is the derivative of one of the variables. The partial derivative, in other words, illustrates how a multivariable function evolves as one of the variables changes. According to the ideal gas equation, PV=kT, a gas’s pressure is determined by both its temperature and its volume. Where P stands for pressure, V for volume, k for constant, and T for temperature. For a constant temperature, partial derivatives are used to determine how the gas pressure varies with volume. In most cases, the partial derivative symbol is a lowercase delta, δ. Before we learn about partial derivative examples, we will first learn about the rules of partial derivatives.
Partial Differentiation and Partial Derivative
The derivative becomes a partial derivative when the function is dependent on two or more variables. When all other variables remain constant, a partial derivative of a function of several variables is common to respect one of the variables. We use all differentiation principles, with the exception that if we are only differentiating for one variable, all other variables are treated as constants.
Let’s say we have a function f(x, y) that depends on two variables, x, and y. x and y are unrelated to one another. The function ‘f’ will thus be said to be somewhat dependent on these two variables. The partial derivative of the function ‘f’ is the derivative of the function ‘f’.
Rules for Partial Derivatives
By splitting more complicated functions into parts, derivative rules allow us to differentiate them. Here are a few of the most important derivative rules to be aware of:
Product Rule:
The partial derivative product rule is a mathematical formula for calculating the derivative of a product of two functions. The partial derivative product rule is written as:
Suppose u and v are two functions of x then the derivative of the product of would be=
The first times the derivative of the second, plus the second times the derivative of the first, is the derivative of a product of two functions.
Quotient Rule:
When all other variables are held constant, the partial derivative of a function at a point x is the derivative of concerning x. The partial derivative quotient rule asserts that the derivative of a function of x divided by the derivative of x to x equals the derivative of y multiplied by y’.
Suppose u and v are two functions of x then the derivative of the quotient u/v would be=
The derivative of a quotient equals bottom times derivative of top minus top times derivative of the bottom, divided by bottom squared.
Chain Rule:
The Partial Derivative Chain Rule is a rule that applies to partial derivative chains.
According to the partial derivative chain rule, the derivative of a function is equal to the derivative of the first function multiplied by the derivative of the second function.
The chain rule is a method for computing the derivative of composite functions, with the number of functions in the components influencing the number of differentiation steps required. If a composite function f(x) is defined as, for example,
f(x)= (g o h)(x) = g[h(x)]
Then f’(x) = g’[h(x)].h’(x)
Because the composite function f is made up of two functions, g and h, you must differentiate f(x) using the derivatives g′ and h′.
Power Rule:
The partial derivative power rule is a mathematical technique for calculating the derivative of a function that is made up of the products of functions that are two or more. According to the Power Rule, the derivative of a function comprised of a product of two or more functions is equal to the derivative of the first function multiplied by the derivative of the second function.
Given that, u = f(x, y), f(x,y), (x, y)n, then, the partial derivative of u concerning x and y will be formulated as:
Ux = n|f(x, y)|n-1 ∂f|∂x
Uy = n|f(x, y)|n-1 ∂f|∂y
Partial Derivative Examples
Example 1:
Find the partial derivative of f(x,y) = x2y + sin x + cos y.
Solution 1:
Now, find out fx first keeping y as constant
fx = ∂f/∂x = (2x) y + cos x + 0
= 2xy + cos x
When we keep y as constant cos y becomes a constant so its derivative becomes zero.
Similarly, finding fy
fy = ∂f/∂y = x2 + 0 + (-sin y)
= x2 – sin y
Example 2:
Find ∂f/∂x, ∂f/∂y, ∂f/∂z for the given function, f(x, y, z) = x cos z + x2y3ez
Solution 1:
To find ∂f/∂x, ∂f/∂y, ∂f/∂z
Given Function: f(x, y, z) = x cos z + x2y3ez
∂f/∂x = cos z + 2xy3ez
∂f/∂y = 3x2y2ez
∂f/∂z =-x sin z + x2y3ez
Example 3:
Determine the partial derivative of the function: f (x,y) = 3x + 4y.
Solution 3:
Given function: f (x,y) = 3x + 4y
To find ∂f/∂x, keep y constant and differentiate the function:
Therefore, ∂f/∂x = 3
Similarly, to find ∂f/∂y, keep x constant and differentiate the function:
Therefore, ∂f/∂y = 4
Conclusion
The partial derivative of a multivariable function is the function’s instantaneous rate of change or slope in one of the coordinate directions. Partial differentiation is computed in the same way as single-variable differentiation, except that all other variables are treated as constants. The partial derivative is a mathematical term for the process of analysing the slope of a surface only in a particular direction at a time. The rate of change of a function of several variables involving one of those variables is calculated using partial derivatives while the other variables are fixed or constant. To put it another way, a partial derivative permits only one variable to vary at a time, which makes it easier to find the minimum and maximum points on surfaces.
 Profile
Profile Settings
Settings Refer your friends
Refer your friends Sign out
Sign out