Profile
Settings
Refer your friends
Sign out
What is a circle?
A circle is a collection of points at equal distances from a common point called its center. We can represent a circle using algebraic and trigonometric equations. We represent the circle’s equation with two variables, giving us:
(x-p)2 + (y-q)2 = c2
Here (p,q) is the coordinate of the circle’s center, and c is the circle’s radius.
However, here, the circle’s equation is an implicit function. The function depends on two different variables. In order to express the points on the circle as a function in the coordinate system, we need two variables. This function is called the circle equation in the implicit form.
If we need to express the circle’s equation as a function of one variable, we need to express the points of the circle as a parametric equation.
Parametric equation of a circle
If we need to express the equation of a circle as a function of one variable, we need to find two equations where we can express x and y as a function of this variable. For this, let us consider the circle shown below.
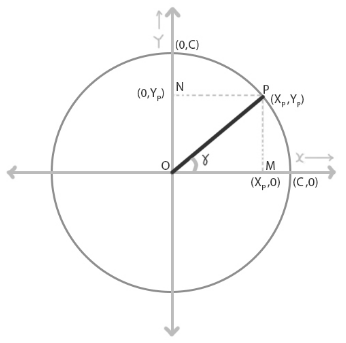
Here we have a circle with radius c with its center coinciding with the coordinate system’s origin. Now let us consider a point on the circle P, that has the coordinates (xp,yp). Let us draw a line connecting this point with the circle’s center. From the figure, we can see that this line makes an Ɣ angle with an x-axis. We will now draw a line parallel to the y-axis to the x-axis from the point (xp,yp).
We will also draw a line from the point (xp,yp) to the y-axis parallel to the x-axis. Now we have a rectangular figure in our representation of the circle.
Now let us take a look at the triangle OPM, the value of sinƔ in this triangle will give us,
⇒ sinƔ = PM/OP
⇒ PM = (sinƔ) x OP
Let us now take a look at the triangle OPN, the value of the angle NPO is Ɣ because they are alternate angles between the two parallel lines.
Now cosƔ in this triangle will give us,
⇒ cosƔ = PN/OP
⇒ PN = (cosƔ) x OP
Here since the quadrilateral figure OMPN is a rectangle,
⇒ PN = OM
Since the length of OM gives us the x coordinate of (xp,yp), we can say that
⇒ xp = (cosƔ) x OP
We can see from the figure above that OP is the radius of the circle, so we can say that
⇒ xp = (cosƔ) x c
Similarly, we can see that the length of PM will give us the length of the y coordinate of (xp,yp).
⇒ yp = (sinƔ) x c
We have expressed xp and yp in terms of Ɣ. So we can now write the coordinate (xp,yp) as ( (cosƔ) x c , (sinƔ) x c ).
Since the point we chose was a random point on the circle, we can express all points of the circle as a function of Ɣ.
So we can say that, x = c (cosƔ)
and, y = c (sinƔ)
This is the parametric equation of a circle.
Now, if we substitute the value of x and y in the implicit form of the circles equation we get,
( c (cosƔ) – p)2 + (c (sinƔ) – q)2
⇒ c2 (( cosƔ – p)2 + ( sinƔ – q)2) = c2
Where c is the circle’s radius.
This shows that the circle’s parametric equation is consistent with the implicit form of the circle’s equation.
Note: In the parametric form of the circle’s equation, we have successfully eliminated the second-degree variable in the implicit form of the circle’s equation using trigonometric functions.
Now the circle’s equation depends only on the value of Ɣ, which goes from 0 to 2π radians.
This Ɣ is called the parametric variable of the circle’s equation.
Properties of circle’s parametric equation
- The circle’s parametric equation can be represented using one variable.
- The parametric variable has a value in the range [0,2π] radians.
- We can derive the implicit as well as the explicit circle’s equation from the circle’s parametric equation.
- The process of changing the circle’s equation from parametric to the explicit form of an equation is called implicitization.
Conclusion
A circle is a collection of points at equal distance from a common point that we call the circle’s center. We can express the circle’s equation in parametric, explicit, and implicit forms.
We use the parametric form of the circle’s equation to express the circle’s equation as a function of a single variable. This single variable is the angle the radius makes with the x-axis. The variable is called the parametric variable. The value of the parametric variable varies in the range [0,2π].
