A well-defined collection of elements or objects is known as a Set. A set is represented by capital letters of alphabets. 

Sets are of two types: 

1. Set-Builder Form
2. Roster Form

Set – Builder Form: In this form, we defined the set with the property of elements.

Roster Form : In this form, all the elements of the set are listed. 

Now in this article, we will discuss the complement of setting its properties and examples, etc.

What is the Complement of Set?

If U is the universal set and set A is the subset of U, then set B which has the elements of U but does not have the elements of set A. Set B is called the complement of set A.

Representation of complement of a set 

Set A is the subset of U, then the complement of set A is represented by A’. 

And, A‘={x:x∈U and x ∉A }

Or, we can also say that the complement of set A is the difference of the Universal set and set A.

A’ = U – A

Method to find the complement of any set

Step – 1: Firstly, read the given problem statement carefully.

Step – 2: Then, write Universal sets and given sets ( for which we have to find a complement ) in roster form.

Step – 3: Then, find the difference between the universal set and the given set.

i.e., A’ = U –A

Step – 4: This difference will be your complement of the given set.

Venn Diagram of Complement of set

We can represent the complement of set by Venn Diagram as shown in following figure

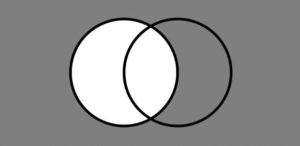
Black shaded rectangular box is considered as a Universal Set, and Set A is shown by white shaded circle, and this is another circle which is interesting, the first circle is representing the Complement of set.

Examples of Complement of a Set

1. Let’s take a Universal set of Natural numbers 1 to 100

And, A is the set which contains all odd numbers between 1 to 100, Then what will be the complement of set A.

Sol : U = { 1, 2, 3, 4, ….. , 100 }

A = { 1, 3, 5, 7, …… , 99 }

Hence, A’ is the set of elements in which all elements are even numbers between 1 to 100.

A’ = { 2, 4, 6, 8, …. , 100}

1. You have a universal set U = { 2,3,4,5,6,7,11,16,17} and A is the subset of U which is given as A = { 3,4,5,6}. What is the complement of set A.

Sol.               U = { 2,3,4,5,6,7,11,16,17}

A = { 3,4,5,6}

A’ = U – A

                              = {2,7,11,16,17}

Hence, We have got A’ as the complement of set A.

1. In a city of 100 people, 60 people are diabetic. Find out the number of healthy persons who are not suffering from diabetic.

Sol.   Set of all peoples of City = U

   Set of diabetic peoples = Z

   No. Of elements in U = n(U) = 100

  No. Of elements in A = n(A) = 60

• Persons who are not suffering from diabetes will be taken in set Y.
• No. Of elements in set Y = n(Y) = 40

And, set Y is the complement of set Z.

1. Let, U is the universal set which consists of all the elements greater than 10 but less than 20. And A and B are the subsets of U and defined as A consists of all the perfect square natural numbers lying between 10 and 20. And B consists of prime numbers between 10 and 20. Find out the complement of both the sets.

 Sol.                                      U = {11,12,13, …. , 19}

Now. We will write both given sets in proper format.

A = {16} (Set of perfect square numbers) 

B = { 11,13,17,19 }

Hence, complement of both sets are given below

A’ = {11,12,13,14,15,17,18,19}

B’ = {12,14,15,16,18}

Properties of Complement of Set

1. If A is the subset of any Universal set then A’ is also a subset of that Universal Set, hence Union of A and A’ will form U.

A A’ = U

1. The intersection of A and A’ will form the empty set which is denoted by ø. 

A A’ =

1. Law of Double Complementation

According to this law, the complement of the set gives the original set.

(A’)’ = A

1.  Law of Empty set and Universal Set

The complement of the Universal set will give the empty set or null set. And, a complement of the Universal Set will give an empty set.

1. De Morgan’s Law 
   1. (A B)’ = A’ ∩ B’

(A ∩B)’ = A’ B’

Conclusion

In this article, we have read about the complement of sets, its properties and examples. We can use Venn diagrams to find Complements of sets which will give you pictorial clarity also. We have talked about the complement and explained it with examples to understand the topic in a better way.