Profile
Settings
Refer your friends
Sign out
According to the definition of an obtuse angle in geometry, ‘an angle whose measure is greater than 90° and less than 180° is known as an obtuse angle.’ A right angle is an angle formed by the intersection of two lines, while a straight angle is an angle formed by the intersection of two lines. Take a look at the obtuse angle that is shown in the example below.
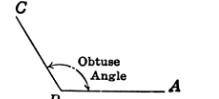
The term “obtuse angle” refers to an angle that is greater than 90 degrees but less than 180 degrees.
The sum of the squares of the two sides of an obtuse angle triangle is less than the square of the longest side of the triangle.
Obtuse angle degree: In the preceding section, we learned that an obtuse angle is defined as an angle that measures less than 180 degrees but more than 90 degrees. Obtuse angle degrees are represented by the numbers 165°, 135°, 110°, 179°, 91°, and so on. As a result, the degree of obtuseness falls between the 90° and 180° ranges of angles.
Obtuse angle in real life: The following are some real-world examples of obtuse angles to consider:
At 4 o’clock, the angle between the hour and minute hands of a clock is 120 degrees.
The angles formed by the blades of a ceiling fan are called blade angles.
Obtuse angle triangle:
When one of the vertex angles of a triangle is greater than 90 degrees, the triangle is referred to as an obtuse angle triangle. An obtuse triangle can be either an isosceles or a scalene triangle, depending on its shape. It is impossible for an equilateral triangle to be obtuse. The longest side of a triangle is the side that is opposite the obtuse angle of the triangle in question. According to the angle sum property of a triangle, a triangle can never be both a right angle and an obtuse angle at the same time. Consequently, we can conclude that if one of the triangle’s angles is obtuse, then the other two triangle’s angles must be acute in order for the triangle to exist.
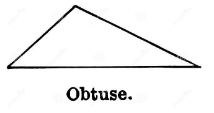
One of the triangles in the diagram above has an angle greater than 90°. As a result, they are referred to as obtuse-angled triangles or just obtuse triangles. In an obtuse angle triangle, the sum of the squares of the two longest sides is less than the sum of the squares of the two shortest sides in an acute angle triangle. When the sides of a triangle measure a, b, and c in such a way that c is the largest side, we have a2 + b2 = c2.
Acute and obtuse angle difference:
Angles can be classified into several categories depending on how they are measured. Angular measurements of less than 90 degrees are referred to as acute angles, whereas measurements of angles greater than 90 degrees but less than 180 degrees are referred to as obtuse angles.
Acute angle | Obtuse angle |
It is less than 90 degrees in measurement. | It has a measurement that is greater than 90 degrees but less than 180 degrees. |
An acute angle triangle is a triangle with three acute angles that are made up of three right angles. | An obtuse angle triangle is a triangle with one obtuse angle and two acute angles, which is called an obtuse angle triangle. |
Examples of acute angles include 56°, 12°, 79°, 43°, and other angles. | Obtuse angles include those of 124°, 179°, 150°, 95°, and other values. |
Conclusion:
Obtuse angles are angles that are always greater than 90 degrees but less than 180 degrees in magnitude. According to the definition of an obtuse angle in geometry, ‘an angle whose measure is greater than 90° and less than 180° is known as an obtuse angle.’
The sum of the squares of the two sides of an obtuse angle triangle is less than the square of the longest side of the triangle. When one of the vertex angles of a triangle is greater than 90 degrees, the triangle is referred to as an obtuse angle triangle. An obtuse triangle can be either an isosceles or a scalene triangle, depending on its shape. In an obtuse angle triangle, the sum of the squares of the two longest sides is less than the sum of the squares of the two shortest sides in an acute angle triangle. Angular measurements of less than 90 degrees are referred to as acute angles.
