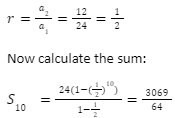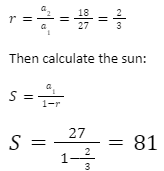A geometric progression or sequence and also known as a geometric series is a sequence of numbers in which the quotient of any two succeeding members of the sequence is a constant called the sequence’s common ratio. The formula x sub n equals a times r to the n – 1 power, where an is the first term in the sequence and r is the common ratio, yields the general term, or nth term, of any geometric sequence. We utilize this formula because writing out the sequence until we reach the required number is not always possible.
Geometric Progression
The geometric progression is a sequence of numbers formed by dividing or multiplying the previous term by the same number. The common ratio is the same or similar number.
Nth Term of Geometric Progression
The ‘nth’ term is a formula that can be used to find any term in a series, where ‘n’ is the term number. Or Any term in a sequence can be found using the nth term rule. Find the difference between each phrase and write this number before the n to get the nth term. Because this series increases in twos, we begin by writing the 2n sequence.
The following is the formula for calculating the general term, nth term, or last term of the geometric progression:
an= nth term
a1=first term
r=common ratio
n=term position
To get the total value of the supplied terms of a geometrical series, apply the formula for the sum of the geometric progression or series. Finite geometric series and infinite geometric series are the two types of geometric series. As a result, there exist several formulas for calculating the sum of terms in a series, which are given below:
Sum of n terms of geometric progression
A geometric series is a set of numbers with a geometric sequence. It is obtained by combining the terms of a geometric sequence.
1. Finite geometric series
The number of terms is n, the first term is a1, and the common ratio is r.
For example: Calculate S10, the 10th partial sum of the infinite geometric sequence 24+12+6+…
Solution: Find r first
2. Infinite Geometric Series
Use the formula to get the sum of an infinite geometric series with ratios with absolute values smaller than one.
S=a1/1-r
The first term is a1, and the common ratio is r.
For example: Calculate the total of the infinite geometric series 27+18+12+8+…
Solution: Find r first:
Conclusion
In this article we conclude that the next number in a geometric progression is obtained by multiplying each integer by the same factor. Any term in a series can be found using the nth term formula. The letter ‘n’ stands for number. By substituting different values for the term number, we can create a series utilizing the nth term (n). in geometric progression, find the nth term. To begin, divide the second term by the first term to get the common ratio r. Then, using the formula an=arn-1 .calculate the nth term using the first term a and the common ratio r.
 Profile
Profile Settings
Settings Refer your friends
Refer your friends Sign out
Sign out