The method of multiplying two vectors is called the cross product. It’s a three-dimensional binary vector operation. The third vector that is perpendicular to the two original vectors is the cross product of two vectors. Its magnitude is determined by the area of the parallelogram between them, and its direction is determined by the right-hand thumb rule. The cross product of two vectors is also known as a vector product because of resultant of the cross product of vectors is a vector quantity. For Example- Using a spanner to twist a bolt: One vector is the spanner’s length. . The direction we apply force to the spanner to tighten or loosen the bolt is another vector. The twist direction that results is perpendicular to both vectors.
Cross Product of Two Vectors
Cross product is a type of vector multiplication in which two vectors of different natures or kinds are multiplied. A vector has both magnitude and direction. Cross product and dot product can be used to multiply two or more vectors. When two vectors are multiplied, the resultant vector quantity is also a vector quantity, The cross product of two vectors, or the vector, is the resultant vector product. The resultant vector is perpendicular to the plane in which the two given vectors are contained.
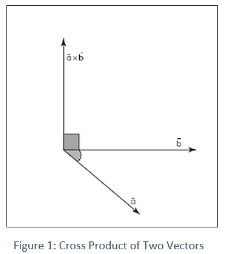
If A and B are two independent vectors, the result of their cross product (Ax B) is perpendicular to both vectors and normal to the plane in which they are both located.
It’s written like this: A × B= |A| |B| sin θ
Cross Product of Two Vectors Matrix
As shown below, the determinant of the matrix can be used to derive the formula for the cross product of two vectors.
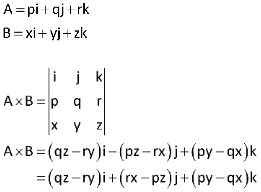
Cross Product of Two Vectors Formula
The area between any two vectors is calculated using the cross product formula. The magnitude of the resultant vector, which is the area of the parallelogram spanned by the two vectors, is determined by the cross product formula.
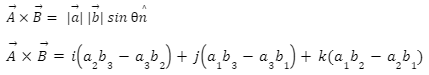
Cross Product of Two Vectors Example
Example: The scalar magnitudes of two vectors are ∣a∣=2√3 and ∣b∣ = 4, respectively, and the angle between them is 60.degree. then Find out the cross product of two vectors.
Solution:
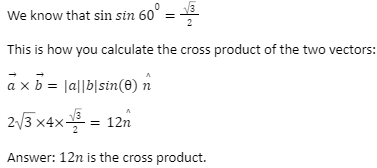
Conclusion
In this article we conclude that a vector that is perpendicular to two vectors is the cross product of two vectors. Both magnitude and direction are present. The resultant vector has the identical magnitude as the parallelogram, whose side lengths are equal to the magnitudes of the 2 given vectors. Cross products are a type of “difference” measure between two vectors in opposition to the dot product which is an evaluation of the uniformity between two vectors. With a cross product, the higher the magnitude of cross product, the more perpendicular two vectors are.
 Profile
Profile Settings
Settings Refer your friends
Refer your friends Sign out
Sign out






