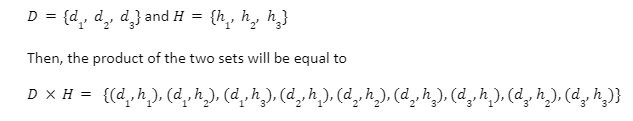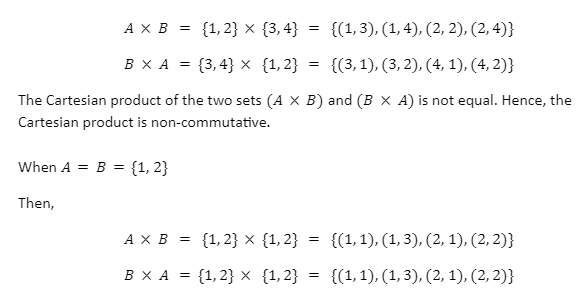Cartesian Product
The ordered product of two non-empty sets is known as the Cartesian product of sets.
Consider two non-empty sets,
Non-Commutativity
The commutative property asserts that the numbers we work with can be relocated or changed from their initial locations without affecting the result. This characteristic applies to addition and multiplication but not to subtraction or division.
Non-commutative operations are binary operations on a set S that do not meet the commutative rule.
Few Examples of Non-commutative Operations
-
Division of numbers, 5÷6≠6÷5
-
Subtraction of numbers, 8-9≠9-8
-
Exponentiation of numbers, 23≠32
-
Vector Product (or cross product) of two vectors, (ab)=-(ba)
Importance of Non-Commutative Operations
These operations are used in day-to-day life, which makes non-commutativity important. A few examples of non-commutative operations in daily life are presented below:
-
Concatenation is a non-commutative procedure that involves connecting two character strings, therefore:
EA + T = EAT ≠ TEA = T + EA
-
When a book is rotated 90 degrees around a vertical axis and then 90 degrees around a horizontal axis, the orientation is different from when the rotations are done in the other sequence
-
When there are two ways to shuffle a deck of cards, A and B, doing A first and then B is not the same as doing B first and then A-it is non-commutative to shuffle a deck of cards
-
Any combination puzzle movements (for example, the twists on a Rubik’s Cube) are non-commutative and group theory can be used to investigate this
The commutative property does not apply to the Cartesian product, because when two sets are multiplied, then the ordered pairs are reversed. The only conditions when the Cartesian product can be equal irrespective of the position of the sets are when either one of the conditions is satisfied.
-
A and B are equal to each other
-
A or B or both are empty sets
To understand non-commutative property in the Cartesian product, let us take an example of three sets:
A = {1, 2}
B = {3, 4}
C = {5, 6}
Then,
Hence, if the value of the two sets is equal, then the Cartesian product of the two sets is commutative.
Non-Associativity
When adding (or multiplying) three or maybe more numbers, this characteristic indicates that the sum (or product) is the same without any regard to how the addends are grouped (or the multiplicands).
Non-associative operations are binary operations on a set S that do not meet the associative rule.
Few Examples of Non-Associative Operations
In case any of the sets is empty, then the product is associative.
What is the value of the set C, when a Set A is multiplied to it, in such a way that their product is commutative?
As discussed above, the only conditions when the Cartesian product can be equal irrespective of the position of the sets is when either one of the conditions is satisfied, thus making the Cartesian product commutative.
-
A and B are equal to each other
-
A or B or both are empty sets
Thus, set C should be an empty set or its value should be equal to Set A.
Conclusion
The commutative property states that the numbers we work with can be moved or changed without affecting the outcome, whereas non-commutativity refers to a mathematical operation that does not obey the commutative property. When three or more integers are added (or multiplied), this property shows that the total (or product) is the same without any regard to how the addends (or multiplicands) are grouped, whereas non-associative properties imply that the mathematical operation does not follow the associative property. The Cartesian product is non-associative as well as non-commutative.
 Profile
Profile Settings
Settings Refer your friends
Refer your friends Sign out
Sign out