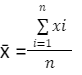Mean Median Mode

Mathematical statistics distinguishes three forms of “averages”: mean, median, and mode. There are many “averages” in statistics, but these are the three most common and likely to be encountered in pre-statistics classes.

The mean, median, and mode can be distinguished as follows:

In statistics, the mean, the median, and the mode are all used to show the central tendency. They tell us in various ways what value in a data set is typical or indicative of the data set.

• Mean

A computation is used to determine the mean, often known as the average value of a data collection. The total number of numbers in the data set divided by the total number of numbers in the data set

• Median

The median is the number in the center of a data collection. Find the Center number by arranging the data points in ascending order. This is the halfway point. The median is the average of two values that are in the center.

• Mode

The mode is the most occurring number in a data collection. We must count how many times each number appears in the data. The mode is the number with the highest frequency. It is OK if there are many modes. If all numbers are repeated  then there is no mode.

How to Find the Mean

• Add up all of the data values to obtain the total
• And then, Count the number of values in your data set
• After that, Divide the total by the number of people
• The mean of a data collection relates to the average value

Mean Calculation Formula

The mean x of a data collection is the sum of all the data divided by the count n.

i.e mean of the observation

How to Calculate the Median

The median x~ is the data value that separates the upper and bottom halves of a data set.

• Firstly, we have to arrange the data values in ascending order from lowest to highest
• The data value in the middle of the set is called the median
• The median of two data values in the Center is the mean of the two numbers

How to Determine Mode

A data mode is the value that appears the most frequently in the presented data, i.e. the observation with the greatest frequency.

Case 1: Data that has not been categorized

For ungrouped data, we just need to determine the most frequent observation. Mode refers to data with the greatest frequency.

For example, the number 6 appears the most in the following data: 6, 8, 9, 3, 4, 6, 7, 6, 3. As a consequence, mode equals 6. The following is a straightforward method for remembering mode: The most frequently entered information. It is important to note that a datum might have no mode, one mode, or numerous modes. Depending on the number of modes, the data can be classed as unimodal, bimodal, trimodal, or multimodal. Because it just has one mode, the offered example is unimodal.

Case 2: Grouped Data

The following procedures can be used to identify the mode when the data is continuous:

Step 1: Identify the modal class, or the class with the highest frequency of occurrence.

Step 2: To determine mode, apply the following formula:

   Mode = 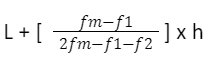 where,

• l = lower limit of the given set,
• f_m is frequency the given set,
• f₁ is frequency of the given set,
• f₂ is frequency of the given set,
• h is the class width.

All the three measures of central values, namely mean, median and mode are related (called an empirical relationship).

{ 3 Median } = 2 Mean  + Mode

For example, if we are asked to determine the mean, median, and mode of continuous grouped data, we may apply the formulae given in the prior sections to obtain the mean and the median, and then use the empirical relation to find the value of mode for given data.

If we have data with a mode of 45 and a median of 35.2, we can find the mean using the previously described mean, median, and mode relations.

2mean + mode = 3 median Or, 2mean = 3 x 35.2 – 45 Or, 2mean = 60.6 Or, mean = 60.6 / 2 = 20.3

Conclusion:

 The arithmetic mean is calculated by adding the numbers and dividing the total by the total number of numbers in the list. This is what most people mean when they say “average.” The median is the value in the center of a list that is sorted from least to biggest. The mode value appears the most frequently on the list.