The terms “mean” and “median” refer to two different types of “averages. A measure of central tendency is a single number that attempts to represent a set of data by finding the central location within that set of data. As a result, central tendency measures are also known as central location measures. They’re classified as summary statistics as well. The mean is probably the most familiar measure of central tendency, but there are others, such as the median. We determine the fundamental position of any data set when describing it.

A data set’s mean is calculated by summing all of the numbers in the set and then dividing by the number of values in the set. The median is the value in the middle of a data set when it is arranged from least to greatest. The number that appears the most frequently in a data set is called the mode.

Definition Mean and median

Mean: The simple mathematical average of two or more numbers is called a mean. The arithmetic mean approach, which utilizes the sum of the numbers in the series, and the geometric mean method, which is the average of a set of products, are two ways to determine the mean for a given collection of numbers. However, most of the time, all of the basic approaches for computing a simple average provide the same approximate result.

Median:

In a sorted list of numbers, the median is the number in the middle. Sort the data in value order from lowest to highest or highest to lowest to find the median value. Although the median can be used to calculate an average or mean, it should not be confused with the genuine mean.

When there are outliers in a series that could have an impact on the average, the median is sometimes used instead of the mean. Outliers have a smaller impact on a sequence’s median than on its mean.

Mean and median formula

1. Mean formula: The mean formula is the sum of the observations divided by the total number of observations. This will aid in the resolution of the vast majority of arithmetic mean-related problems. The mean formula for a set of observations is as follows:

Mean= (sum of observations) / Total no. of observations

The sum of all the data in a data set is divided by the count n to get the mean x̄

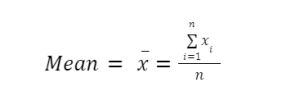
The mean value of the supplied data set is x̄

n is the total number of frequencies.

2. Median formula: We must arrange the data in ascending or descending order in order to get the median. Get the total number of observations in the data after you have organized it.

The median is (n+1)/2 if the number is odd. If the number is even, use the formulas n/2 and (n/2) + 1 to obtain the two middle terms. Calculate the average of these two middle terms. For even numbers, the median formula is: Median = ((n/2)th term + ((n/2) + 1)thterm)/2

For grouped data, we have the median formula. For grouped data, the median formula is as follows:

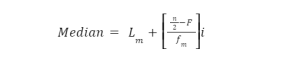
n = Number of occurrences

F = Prior to the median class, the cumulative frequency of each class.

f_m = Frequency of the median of the class

L_m = Lower border of the class median

i = Class width

Mean and median uses

Uses of mean & median are given below:

• The mean can be used to get a sense of the data set as a whole or a picture of it. The mean is the best option for a data set with numbers that are close together. The median can be used to discover which values are higher than and lower than the midpoint.
• The median is important because it represents the location of the dataset’s centre value. The median is more useful to compute than the mean when a distribution is skewed and/or contains outliers.

Conclusion

When a set of data is arranged in ascending or descending order, the mean is the average value, and the median is the middle value. When the distribution of data values is symmetrical & there are no obvious outliers, the mean is the finest option. When the distribution of data values is skewed or there are obvious outliers, the median is the best option.