Calculus allows one to determine both maximums and minimums by applying the concept of derivatives. Because we are familiar with the idea that the derivatives provide information about the gradient and the slope of the function, we are able to identify the points along with the function at which the gradient is zero. These points are referred to as turning points or stationary points. These are the points that are connected to the values of the function that are (locally) the greatest or the least.

Maxima and Minima Points

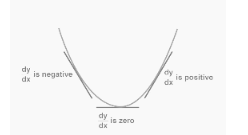
The figure for the curve that contains stationary points can be found further down. As a result, it is clear from looking at the figure that the slope was negative before it became zero, but that after it became zero, the slope turned positive. Before the stationary point, dy/dx is said to be negative, while after the stationary point, it is said to be positive. Because of this, we can conclude that d²y/dx² has a positive value at the stationary point shown below. Because of this, we can also conclude that the point of minimum exists wherever the double derivative has a positive value. When looking at the curve from the opposite direction, the point of maximum occurs wherever the double derivative has a negative value. The second derivative test is another name for this particular evaluation.

Let there be a function denoted by the letter f that is defined on the open interval I.

Let’s assume that f is uninterrupted at the crucial point c in I.

If the sign of f'(x) does not change as x increases through c, then c is neither a point of local maxima nor a point of local minima. If this is the case, then c is a point of local extrema. A point like this is referred to as a point of inflection.

Stationary Points vs Turning Points

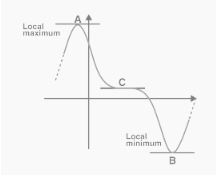
The points along a graph at which the slope is equal to zero are referred to as stationary points. In other words, the tangent of the function will become horizontal, which will be represented by the equation dy/dx = 0. The figure that is shown below A, B, and C contains information on all of the stationary points. And the points at which the function changes its path; for example, if it was going upward, then it will go downward, and vice versa; points A and B are turning points because the curve changes its path at those points. However, despite the fact that the graph remains horizontal for a relatively brief period of time after point C, the slope of the line continues to decline from left to right.

Derivative Tests

The maximum and minimum values of any function can be determined with the assistance of the derivative test. The tests that are utilised most frequently are the first-order derivative test and the second-order derivative test. Let’s take a closer look at this matter.

First Derivative Test

Let’s say that the function that is defined in the open interval I is denoted by f. And let f be an unbroken function at the critical point c in I such that f'(c) equals 0.

1. If the value of f'(x) goes from being positive to being negative as x continues to increase through point c, then point c is the point where the local maximum occurs. And the f(c) represents the highest possible value.
2. The point of local minima is point c if the function f'(x) flips its sign from negative to positive as x continues to increase through that point. And the smallest possible value is denoted by the f(c).
3. If there is no change in the sign of f'(x) as x continues to increase through c, then c is not a point of either a local or a local maximum. It will be referred to as the point of inflection from this point forward.

Second Derivative Test

Let f represent the function that is defined on interval I, and assume that it can be differentiated in two ways at c.

i. The point of local maxima will be x = c if and only if f'(c) = 0 and f”(c) <0. Then f(c) will have a value that is the highest possible in the local area.

ii. If f'(c) equals 0 and f”(c) is greater than 0, then x = c will be the point of local minima. If this is the case, f(c) will have a value that is closer to the local minimum.

iii. The hypothesis is not supported when both f'(c) = 0 and f”(c) = 0. The value of the local maximum and minimum can be determined with the help of the first derivative test.

The characteristics of both maxima and minima

1. If f(x) is a continuous function in its domain, then at least one maximum or one minimum should lie between equal values of f(x).
2. Maximums and minimums appear in an alternating fashion. In other words, there is one maximum located between two minima, and vice versa.
3. If f(x) tends to infinity as x tends to an or b and f'(x) = 0 only for one value x, i.e. c between a and b, then f(c) is the minimum and the least value. This is because f(c) is the only value for which both f(x) and f'(x) are equal. If f(x) tends to –∞ as x tends to an or b, then the maximum and highest value of f(c) is the case.

Conclusion

The points along a graph at which the slope is equal to zero are referred to as stationary points. In other words, the tangent of the function will become horizontal, which will be represented by the equation dy/dx = 0.  And the points at which the function changes its path;  are turning points because the curve changes its path at those points. If f(x) is a continuous function in its domain, then at least one maximum or one minimum should lie between equal values of f(x). Maximums and minimums appear in an alternating fashion. In other words, there is one maximum located between two minima, and vice versa.