The extrema of a function are the points at which the function reaches its maximum and minimum values. The maximum and minimum values of a function are the maximum and minimum values of the function within the supplied set of ranges, respectively. Under the whole range of the function, the absolute maxima and minima of the function are known as the absolute maxima and minima, respectively, and the maximum value of the function is known as the absolute maxima.
It is possible to have multiple maximum and minimum values for a function that are not the absolute maximum and minimum values of the function. These additional maximum and minimum values are referred to as local maxima and minima. Now, let’s go over some more concepts such as local maximum and minimum values, absolute maximum and minimum values, as well as how to find the maximum and minimum values of a given function.
The maxima and minima values of a function
The peaks and valleys of a function’s curve are referred to as its maxima and minima. For a function, the maximum and minimum values can be any number of times. It is possible to find the maximum and minimum values of any function in calculus, without even having to look at its graph. The maximum point on the curve will be the highest point within the specified range, and the minimum point on the curve will be the lowest point within the supplied range.
Extrema is a term used to describe the combination of maximum and minimum values. Various peaks and valleys may be seen in the graph depicted in the figure provided below. Maximum and minimum values of the function are obtained at x = a and x = 0, respectively, while maximum and minimum values of the function are obtained at x = b and x = c. All of the peaks are the maxima, and all of the valleys are the minima of the landscape.
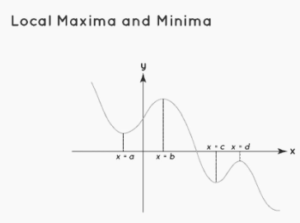
Local Maxima and minima
Local maxima and minima are the maximum and minimum values of a function that occur within a specific interval of time. As an example, a function’s value at one point in time would be the value of the function at that point in time, for which the values of the function near that point are always less than the value of the function at that moment. Local minima, on the other hand, would be the value of the function at a place where the values of the function near that point are greater than the value of the function at that position, and this is what is meant by local minima.
•The point x = b is a point of local maximum for the function f(x) if it is in the neighbourhood of b, that is in the range(b−𝛿, b+𝛿) where 𝛿 can be made arbitrarily small, and f(x) <f(b) for all x ∈ (b−𝛿, b+𝛿)/{b}. This simply indicates that, if we consider a tiny region (interval) about x = b, f(b) should be the largest value in that interval
•At point x = a, that is, in the range (a−𝛿,a+𝛿), f(x) > f(a) for all x∈(a−𝛿,a+𝛿)/{a} is a point of local minimum for f(x) , is the point of local minimum for f(a) is the point of local minimum for the function f(x). Thus, if we consider a tiny interval surrounding x = a, we should expect f(a) to be the smallest value in that interval
When looking at the image below, we can see that the local maxima and minima are represented by x = b and d, and the local maxima and minima are represented by x = a and c, respectively.
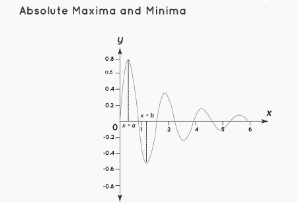
Absolute Maxima and Minima
The absolute maxima and minima of a function are the points at which the function reaches its maximum and minimum values within its entire domain, respectively. The absolute maxima and minima of a function are the points at which the function reaches its minimum and maximum values within its entire domain, respectively. Throughout the whole domain, there can only be one absolute maximum of a function and one absolute minimum of a function for that function. Alternatively, the absolute maximum and minimum values of a function can also be referred to as the global maximum and maximum values of a function, respectively.
•Absolute maxima are as follows: In the case when f(x)≤ f(a) for all x∈D (the domain of f(x)), the point x = A is a point of global maximum for f(x)
•The absolute minima: In the case of f(x), if f(x)≥f(a), then x = a is the global minimum of f(x) for all x∈D (the domain of f(x)
The point x = a represents the absolute maximum of the function, while the point x = b represents the absolute minimum of the function in the picture below.
Conclusion
The extrema of a function are the points at which the function reaches its maximum and minimum values. The maximum and minimum values of a function are the maximum and minimum values of the function within the supplied set of ranges, respectively. The peaks and valleys of a function’s curve are referred to as its maxima and minima. For a function, the maximum and minimum values can be any number of times. Local maxima and minima are the maximum and minimum values of a function that occur within a specific interval of time. The absolute maxima and minima of a function are the points at which the function reaches its maximum and minimum values within its entire domain, respectively.
 Profile
Profile Settings
Settings Refer your friends
Refer your friends Sign out
Sign out