Profile
Settings
Refer your friends
Sign out
Definition
We will define the Logarithm function as,
logba = c (where, a>0 , b>0, a ≠ 1 )
a = bc (necessary condition) (And this is also exponential form)
Here, b is the base of this logarithm function, also we can read this as “log base b of a”.
Common bases = 10 and e.
- Log with base 10 is a Common Logarithm.
- Log with base e is Natural Logarithm.
- In Computer Science, Log with base 2 is widely used which is known as Binary Logarithm.
Logarithm Table
For finding log values, we can use a log table. In the log table, we can find log values very easily.
Before knowing about the use of the logarithm table, we should know about some more concepts of the Logarithm function, which are described below.
Logarithm function has two parts, Characteristic and Mantissa.
- Characteristic: This is an integral part of the logarithm function.
- Mantissa: This is the decimal part.
It is necessary that we always take the Mantissa part positively.
logab = integer + fraction(positive value)
Then, b = antilog(mantissa) + characteristic
Log Table 50 to 100-
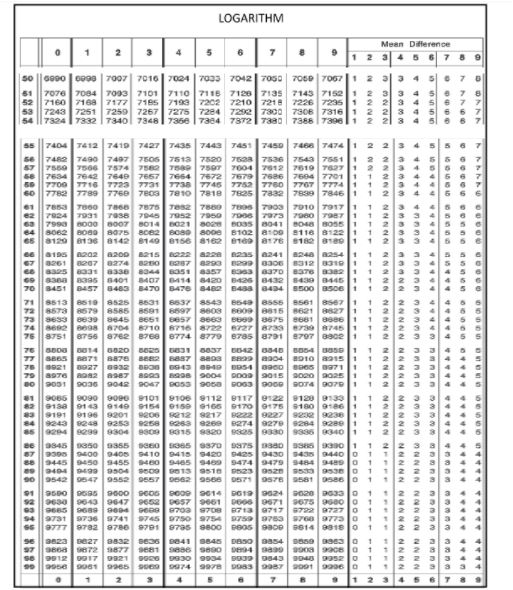
How To Use Log Table:
Here a step-by-step process is given for finding the log values using a log table.
Step 1: For different bases, different log tables are used. So, for finding the log value, firstly see the base of the log function.
Step 2: Separate the characteristic part and mantissa part of the given number.
y = 14.21
Characteristic = 14, Mantissa = 21
y = -12.78
Characteristic =-12, Mantissa = 78
Step 3: If I talk about the Common Logarithm table, that is log base 10.
Now, you should round off your digit with two places of decimal.
Step 4: you have y = 14.21, you have to find its value using the log table.
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | MEAN DIFFERENCE | |||
| 1 2 3 | 4 5 6 | 7 8 9 | |||||||||||
| 14 | 1461 | 1492 | 1523 | 1553 | 1584 | 1615 | 1644 | 1673 | 1703 | 1732 | 3 6 9 | 12 15 18 | 21 24 27 |
A Part of log table for finding the value
- You have an Integer part is 14, then find this integer part in the very first column, that is mentioned below.
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | Mean Difference | |||
| 1 2 3 | 4 5 6 | 7 8 9 | |||||||||||
| 14 | 1461 | 1492 | 1523 | 1553 | 1584 | 1615 | 1644 | 1673 | 1703 | 1732 | 3 6 9 | 12 15 18 | 21 24 27 |
- Now, check the decimal part of the number. We have to check Digit at the first decimal place in the log table in specified columns like, we have 2 in our example, so we have to take a number which is written in Column of 2.
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | Mean Difference | |||
| 1 2 3 | 4 5 6 | 7 8 9 | |||||||||||
| 14 | 1461 | 1492 | 1523 | 1553 | 1584 | 1615 | 1644 | 1673 | 1703 | 1732 | 3 6 9 | 12 15 18 | 21 24 27 |
So, we get the digit 1523.
- Digit at 2nd decimal place should check in the Mean Difference column.
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | Mean Difference | |||
| 1 2 3 | 4 5 6 | 7 8 9 | |||||||||||
| 14 | 1461 | 1492 | 1523 | 1553 | 1584 | 1615 | 1644 | 1673 | 1703 | 1732 | 3 6 9 | 12 15 18 | 21 24 27 |
Now, we get the digit 3.
Step 5: You have two digits obtained by Step 4, so the next step is to add both digits.
1523 + 3 = 1526
We have got Mantissa part of the log value.
Step 6: Our next task is to find the Characteristic part of log value.
We have the number 14.21 which is between 10 and 100 (that is 10 1 and 102), so the characteristic part will be 1.
OR
You can find the characteristic part for base 10 values, using the following method.
CHARACTERISTIC PART = (Total Number of digits at left place of decimal) – 1
which also gives 1 as our characteristic part in our example.
Step 7: Now you have characteristic and mantissa parts for getting log values, s you will have to combine these values.
And the log value for 14.21 is,
Conclusion
Log Functions are just inverse of the exponential function. We also have many real-life applications of a logarithm. Also, if a person learns the use of a log table, then she or he can easily find log values, but every time you will not have a log table so that’s why the properties of log also make it easier to solve log problems.
