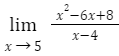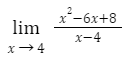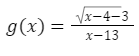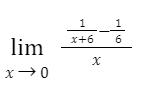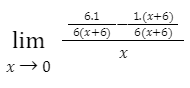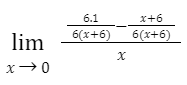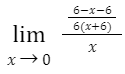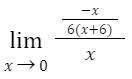In mathematics, limits are the values at which a function approaches the output for the given input values. Limits are used to define integrals, derivatives, and continuity in calculus and mathematical analysis. It is used during the analysis process and always refers to the behaviour of the function at a specific point. The concept of the limit of a topological net generalises the concept of the limit of a sequence and is related to the limit and direct limit in the theory category.
What is the limit of a function
The value that the function approaches as its argument approaches the limit of a function at a point and in its domain. The concept of a limit is at the heart of calculus and analysis. It is used to define the derivative and the definite integral, as well as to examine the local behaviour of functions near points of interest.
Informally, a function is said to have a limit L at a if it is possible to arbitrarily close the function to L by selecting values closer and closer to a. It should be noted that the actual value at a has no bearing on the value of the limit.
The following is the notation-
Which refers to “the limit of f(x) as x approaches a is L.”
Finding the limits of a function
If you need to find the algebraic limit of a function, you have four options: plugging in the x value, factoring, rationalising the numerator, and finding the lowest common denominator.
if the function is continuous at the x value at which the limit is taken. If the function is undefined at this xvalue, we must proceed to the other techniques to simplify your function so that you can plug in the approached x value.
1. By entering the x value, we can find the limit.
The first method for algebraically solving for a limit is to plug the number that x is approaching into the function. If we get an undefined value 0 in the denominator, you must try another technique. But if function is continuous at that x value, we will get a value and you’re done; we have found your limit. For example, using this method, you can discover the following limit:
Because f(5) = 3 and this function is continuous at x = 5, the limit is 3.
2. By factoring, you can find the limit.
When plugging in fails, try factoring — especially if any part of the given function is a polynomial expression.
When we first try to plug 4 into the function, we get 0 in the numerator and denominator, indicating that you should move on to the next technique. The quadratic expression in the numerator begs we to factor it. Take note that the previous function’s numerator factors to (x – 4)(x – 2). On the top and bottom of the fraction, the x – 4 cancels. This step results in f(x) =x – 2. we can get 2 by plugging 4 into this continuous function.
3. By rationalising the numerator, find the limit.
The third method for finding limits algebraically requires rationalising the numerator. This method is required for functions with a square root in the numerator and a polynomial expression in the denominator. Assume you’ve been asked to find the limit of this function as x approaches 13:
When we plug in numbers, we get a 0 in the fraction’s denominator. Factoring fails because there is no polynomial to factor in the equation. In this case, multiplying the numerator and denominator by the numerator’s conjugate cancels out the problematic term in the denominator, and we can find the limit.
Multiply the fraction’s top and bottom by the conjugate: The numerator’s conjugate is
√(x-4) + 3
When we multiply through, we get the following setup:
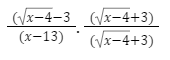
To obtain, multiply the terms in the numerator using the first, outer, inner, and last (FOIL) technique.
(x-4) + 3√(x-4) – 3√(x-4) – 9
Which reduces to x – 13 the middle two terms cancel and we combine like terms from the FOIL.
Factors to cancel: Cancelling results in the following expression:
The (x – 13) terms cancel, yielding the following result:
Calculate the limits: For example, when you enter 13 into the function, you get 1/6, which is the limit.
4. Find the limit by locating the lowest common denominator
We use the fourth and final algebraic limit-finding technique when given a complex rational function. The plugging technique fails because we end up with a 0 in one of the denominators. The function cannot be factored, and there are no square roots to rationalise. As a result, we know it’s time to move on to the final technique. We combine the functions using this method by locating the lowest common denominator (LCD). When the terms cancel, you can find the limit.
For example, to find the limit, follow these steps:
Locate the LCD of fractions on the top:
Distribute the denominators on top:
Add or subtract the numerators before cancelling the terms: Subtraction of the numerators yields
Simplify this
To make things even easier, apply the fraction rules:
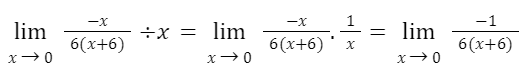
Simplify by substituting the limit value into this function. Then the limit as x approaches zero, so the limit here is –1/36.
Conclusion
We conclude in this article that a limit is the value that a function approaches as its inputs get closer and closer to some number. The concept of a limit is at the heart of all calculus. Limit, a mathematical concept based on the concept of closeness, is primarily used to assign values to certain functions at points where no values are defined, so that they are consistent with nearby values.
 Profile
Profile Settings
Settings Refer your friends
Refer your friends Sign out
Sign out