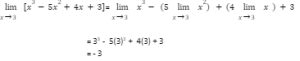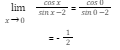In this, we will discuss the existence of limits, expansion in evaluating limits, evaluation of algebraic limits, etc. We will also get a brief on continuity and differentiability as well.
Generally, the limit of a function is written as:
Here x→c denotes the value of x that is tending to c.
Here the limit of the function is said to exist only when the right-hand limit is equal to the left-hand limit of the function.
Properties of Limits
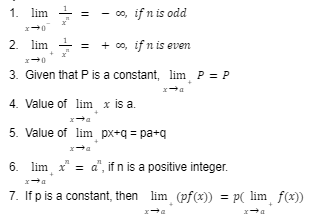

Some Standard Limits:
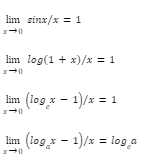
Estimating a limit using a graph
Now that we know how to identify a limit in a simple equation, let’s see how to identify a limit.
Although the equation looks different than the one we initially saw, the fundamental concept remains the same.
X is the variable, f(x) is the limit.
Let’s look at what the graph equation is supposed to represent.
How did we arrive at this point on the graph, though?
Let’s try to understand what the graph represents visually.
- The graph runs through 2 for the value of +x at all instances on x on the graph.
- The graph coincides at one point, which is 0=3 for all values of x approaching 3. This will hold true for ANY value for the limit as f(3)=0 has no value on the limit of x as it approaches 3.
- We know the limit for f(x)=2 for all instances, except for when x=3, so we can safely assume that the limit, f(x), is 2.
What is continuity?
Qualitatively the graph of a function is said to be continuous at x = d if travelling along with the graph of the function and crossing over the point at x = d either from left to right or from right to left, and one does not have to lift his pen. If one has to lift his pen, the function’s graph breaks or gets discontinued at x = d.
A function f(x) is continuous at x = d, if
onsectetur adipiscing elit. Ut elit tellus, luctus nec ullamcorper mattis, pulvinar dapibus leo.
i.e. Left-Hand limit = Right-Hand Limit = value of the function at x = d
Otherwise, the function f(x) is a discontinuous function. The theory of limit and continuity is one of the essential terms to understand calculus. A limit is stated as a number that a function achieves when the independent variable of the function approaches a given value.
What is Differentiability?
A function f(x) is explained to be differentiable at the point x = d if LHD=RHD and both are limited values, and the function is continuous at d.
The function f(x) is said to be non-differentiable at x = d if
(a) Both R.H.D & L.H.D exist but are not equal.
(b) Either or both R.H.D & L.H.D are not limited.
(c) Either or both L.H.D & R.H.D do not exist.
(d) The function is not continuous at d.
Conclusion
Limits are important in calculus. This can help determine the continuity of a particular function and its differentiability. Limits can also be applied to other functions, showing how the function behaves when it approaches infinity. Here, we learned about limits, properties of limits, the existence of limits, expansion in evaluating limits, some of the essential expansions, evaluation of algebraic limits, continuity, and differentiability.
 Profile
Profile Settings
Settings Refer your friends
Refer your friends Sign out
Sign out