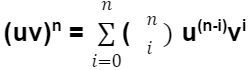Profile
Settings
Refer your friends
Sign out
The Leibnitz rule for derivative of the antiderivative is essentially what this theorem is about. In accordance with the rule, the derivative in nth order of the product of two functions may be stated mathematically with the assistance of an equation. Antiderivatives (also known as primitives) of a function are functions that might have been used to calculate the derivative of a function if the function had been supplied. All of these antiderivatives may be found using a formula known as the indefinite integral of the function, and the process of discovering antiderivatives is referred to as an integration of the function.
Leibniz Rule
The Leibniz rule of differentiation is a generalisation of the product rule of differentiation. According to the Leibniz rule, if two functions f(x) and g(x) are differentiable n times separately, then their product f(x) is also differentiable n times (x). g(x) is likewise differentiable n times in the same way. Polynomial functions, trigonometric functions, exponential functions, and logarithmic functions are examples of functions that can be used. Let us generalise the Leibniz rule using the formula shown below.
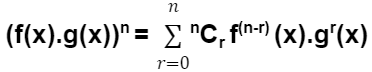
Here nCr = n!(r!.(n−r)! and n! = 1 × 2 v 3 × 4 × ….(n – 1) × n.
For the most part, the Leibniz rule is used to calculate the derivative of the product of two functions. If f(x) and g(x) are functions, then the first derivative of the product of these functions is equal to the sum of their first derivatives. If f(x) is an integer, then the first derivative is equal to the product of their first derivatives. If g(x) is an integer, then the first derivative is equal to the product of their first derivatives.
(f(x).g(x))’ = f'(x).g(x) + f(x).g'(x)
To further our investigation, we may employ the Leibniz rule to get the second derivative resulting from the product of two functions. For the second derivative of the product of two functions, f(x) and g(x), the Leibniz rule for the second derivative may be thought of as being analogous to the binomial expansion of a pair of terms of the second degree. Let’s also look at the second derivative of the product of the functions as a reference point.
(f(x).g(x))” = f”(x).g(x) + 2f'(x).g'(x) + f(x).g'(x)
The leibniz rule may be used to compute the product of several functions as well as the derivatives of a large number of functions. The mathematical induction method can be used to show the Leibniz rule.
Leibnitz Theorem Formula
Imagine there exist two functions, u(t) and v(t), which have derivatives up to the nth order, and the derivatives of these two functions are equal. Consider the derivative of the product of these two functions, which is the derivative of the product of these two functions.
The first derivative might be expressed as follows:
(uv)’ = u’v+uv’
We may now take the second derivative of the preceding statement by differentiating it once again.
(uv)’’
= [(uv)’]’
= (u’v+uv’)’
= (u’v)’+(uv’)’
= u′′v + u′v′ + u′ v′ + uv′′
= u′′v + 2u′v′ + uv′′
We can do the same thing with the third derivative.
(uv)′′′
= [(uv)′′]′
= (u′′v + 2u′v′ + uv′′)′
= (u′′v)′ + (2u′v′)′ + (uv′′)′
= u′′′v + u′′v′ + 2u′′v′ + 2u′v′′ + u′v′′ + uv′′′
= u′′′v + 3u′′v′ + 3u′v′′ + uv′′′
When we compare these two formulations, we see that they are quite close to the binomial expansion increased to the exponentiation level. By taking into consideration the components with zero exponents, u0 and v0, which correspond to the functions u and v themselves, we can obtain the formula for the nth order of the derivative product of two functions, which is written as
Where ( in ) represents the number of i-combinations on n elements.
This formula is referred to as the Leibniz Rule formula, and it may be demonstrated by induction.
Conclusion
The Leibnitz theorem, often known as the Leibniz integral rule for derivation, is a mathematical concept that is represented by the integral sign. It was given its name in honour of the well-known scientist Gottfried Leibniz. As a result, the theorem is primarily intended for use with the derivative of the antiderivative. Essentially, the Leibnitz theorem is used to generalise the product rule of differentiation, which is a mathematical concept. If there are two functions, let them be a(x) and b(x), and if they are both differentiable independently, then their product a(x) is a function of the x variable (x). b(x) is also differentiable up to n times.
