The ratios of the lengths of the sides of a triangle are known as trigonometric ratios. These ratios in trigonometry shows the connection between the ratio of sides of a right triangle to the angles of the triangle. Sin, cos, and tan, or sine, cosine, and tangent ratios, are the six trigonometric ratios. The sin, cos, and tan can be used to calculate the other key trigonometric ratios, cosec, sec, and cot.

The name “trigonometry” comes from the Greek words “trigonon” and “metron,” which both mean “to measure.” It’s a branch of mathematics that deals with the relationship between a right-angled triangle’s angles and sides. Trigonometry is, in reality, one of the oldest sciences studied by experts all over the world. 

Trigonometric Ratios 

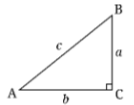
The six trigonometric ratios in trigonometry are sine, cosine, tangent, secant, cosecant, and cotangent. In summary, these ratios are sin, cos, tan, sec, cosec, and cot. Consider the right-angled triangle in the diagram below. Trigonometric ratios can be used to calculate the ratios of any two of the three sides of a right-angled triangle in terms of their respective angles. The values of these trigonometric ratios can be calculated using the acute angle measure in the right-angled triangle shown below. This indicates that angle C determines the value of the ratio of any two triangle sides. Alternatively, we can calculate the values of these trigonometric ratios for angle A. In that situation, only the base and perpendicular will swap for the specified right triangle.

The following are the six trigonometric ratios:

• The sine ratio is defined as the ratio of the perpendicular to the hypotenuse for any given angle. The sine of the angle in the given triangle can be written as sin = AB/AC.
• The cosine ratio is defined as the ratio of the base to the hypotenuse for any given angle. The cosine of the angle in the given triangle can be written as cos = BC/AC.
• The tangent ratio is defined as the ratio of the perpendicular to the base for any given angle. The tangent of an angle in the given triangle can be written as tan = AB/BC.
• The cosecant ratio is defined as the ratio of the hypotenuse to the perpendicular for any given angle. The cosecant of angle in the given triangle can be written as cosec = AC/AB.
• The secant ratio is defined as the ratio of the hypotenuse to the base for any given angle. The secant of angle in the given triangle can be written as sec = AC/BC.
• The cotangent ratio is defined as the ratio of the base to the perpendicular for any given angle. The cotangent of angle in the given triangle can be written as cot = BC/AB.

Trigonometric ratio formulas 

Trigonometric ratios can be calculated using the ratio of any two sides of a right-angled triangle. Given the measure of the other two sides, we may use the Pythagoras theorem to calculate the third side. To compare the length of any two sides with the angle in the base, we can utilise the abbreviated form of trigonometric ratios. The angle is sharp (90o) and is generally measured in the anticlockwise direction with reference to the positive x-axis.

• Sin θ = Perpendicular/Hypotenuse
• Cos θ = Base/Hypotenuse
• Tan θ = Perpendicular/Base
• Sec θ = Hypotenuse/Base
• Cosec θ = Hypotenuse/Perpendicular
• Cot θ = Base/Perpendicular

Let’s look at the reciprocal trigonometric ratio formulas for the trigonometric ratios described previously. We can see that sin is a reciprocal of cosec, cos is a reciprocal of sec, tan is a reciprocal of cot, and vice versa as we see.

• Sin θ = 1/cosec θ
• Cos θ = 1/sec θ
• Tan θ = 1/cot θ
• Cosec θ = 1/sin θ
• Sec θ = 1/cos θ
• Cot = 1/ tan

Trigonometric Ratio Table

Many trigonometric ratio tables are used to make calculations easier and simpler.

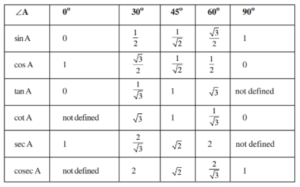
These are some of the specific values of trigonometric ratios.

Conclusion

• If the angle keeps the same, the values of trigonometric ratios do not change when the side lengths of the triangle change.
• All the trigonometric functions are periodic in nature.
• The missing sides or angles in a triangle are found using trigonometric ratios.