Profile
Settings
Refer your friends
Sign out
The rule of sines provides the link between an oblique triangle’s sides and angles (non-right triangle). In trigonometry, the law of sines and the law of cosines are critical laws for “solving a triangle.” The sine rule states that the ratios of a triangle’s side lengths to the sine of its opposing angles are equal.
Law of Sines
The ratio of a triangle’s side and matching angle is equal to the diameter of the triangle’s circumcircle. As a result, the sine law may be expressed as
a/sinA = b/sinB = c/sinC = 2R.
- Here, a, b, and c denote the lengths of the triangle’s sides.
- A, B, and C represent the triangle’s angles.
- R is the radius of the triangle’s circumference.
Law of Sines Formula
The law of sines is used to calculate the lengths of a triangle’s sides in relation to the sines of consecutive angles. It is the ratio of the length of the triangle’s side to the sine of the angle created by the remaining two sides. The law of sines formula is applicable to all triangles except the SAS and SSS triangles.
It states that a/sin A = b/sin B = c/sin C, where a, b, and c are the triangle’s lengths and A, B, and C are the triangle’s angles.
This formula may be expressed in three ways:
- a/sinA = b/sinB = c/sinC
- sinA/a equals sinB/b equals sinC/c
- a/b equals sinA/sinB; a/c equals sinA/sinC; b/c equals sinB/sinC
Proof of Law of Sines Formula
Given two angles and aside, the law of sines is used to calculate the remaining sides of a triangle. This is referred to as triangulation. Additionally, it may be used when given two sides and one of the non-enclosed angles. However, in certain of these circumstances, referred to as the ambiguous case, the triangle cannot be established uniquely using the available data, and we have two alternative values for the enclosed angle. To demonstrate the sine law, consider the following two oblique triangles.
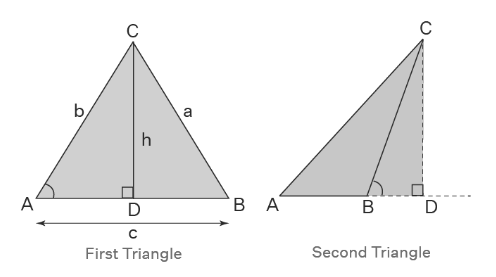
In the first triangle we have: h/b = sinA
⇒ h = b sinA
In the second triangle we have: h/a = sinB
⇒ h = a sinB
Additionally, sin(180o – B) = sinB.
By equating the h values in the preceding formulas, we obtain:
a sinB = b sinA
⇒ a/sinA = b/sinB
Likewise, we can infer a relationship between sin A and sin C.
asinC = csinA
⇒ a/sinA = c/sinC
By combining the two formulas above, we obtain the sine law shown below.
a/sinA = b/sinB = c/sinC
Applications of Sine Law
The law of sines is useful for determining the missing side or angle of a triangle when all other necessary data is available. The sine law may be used to determine the following:
- The length of a triangle’s side using ASA or AAS criteria.
- The unknown angle of a triangle; and
- The triangle’s area.
Law of sines in Real life
- In real life, the law of sines is employed to determine the angle of tilt in engineering.
- In astronomy, it is used to determine the distance between planets or stars.
- Additionally, navigation may be quantified using the law of sines.
Law of sines and Cosines
Both the law of sines and the law of cosines are used to determine an unknown angle or side of a triangle. Let us examine the distinction between the two laws.
The sine law
It is utilized when we are given two angles and a side, or when we are given two sides and an included angle.
Cosine law
It is employed when we are given three sides or two sides plus an angle.
Conclusion
When two angles and a side are known, the rule of sines may be used to compute the remaining sides of a triangle—a process known as triangulation. Additionally, it may be employed when two sides and one of the open angles are known.
