The law of cosines establishes a relationship between the lengths of a triangle’s sides and the cosine of one of its angles. We may now acquire values for distances and angles that cannot be measured in any other way using trigonometry. The law of cosines is useful for calculating the third side of a triangle given two sides and their enclosed angle, as well as for calculating the angles of a triangle if we know all three sides. A triangle is composed of six elements: three sides and three angles. Let us first grasp the law of cosines and its derivation in order to investigate the interrelationships between these parts using the cosine function.
Law of Cosines
The law of cosine says that the square of any one of a triangle’s sides is equal to the difference between the sum of the squares of the other two sides and twice the product of the other two sides and the cosine angle contained between them.
Let a, b, and c denote the lengths of the triangle’s three sides, while A, B, and C denote the triangle’s three angles. Then, according to the rule of cosine, a2 = b2 + c2-2bc·cosA. As stated previously, in trigonometry, the rule of cosines generalises the Pythagorean theorem. What happens if you substitute 90o for the angle in one of the rules? Due to the fact that cos 90o = 0, we are left with Pythagoras’s theorem.
The cosine law is often referred to as the cosine rule. This rule is important for resolving any triangle’s missing information. For instance, if you know the lengths of two sides of a triangle and the angle between them, this rule aids in determining the length of the triangle’s third side. In the next sections, we will examine several cosine law formulations and the procedure for locating these missing parameters.
Law of Cosines Formula
When the triangle’s two sides and included angle are known, the law of cosines formula may be used to calculate the missing side, i.e., in the case of a SAS triangle. We already know that if A, B, and C are the triangle’s vertices, their opposing sides are denoted by the little letters a, b, and c. The law of cosines formula can be used to:
- When b, c, and A are given, find a (or)
- When a, c, and B are given, find b (or)
- When a, b, and C are given, find c (or)
- Given a, b, and c, find any angle of the triangle.
There are three laws of cosines, and based on the given data, we select one to solve our difficulties.
- a2 = b2 + c2 – 2bc·cosA
- b2 = c2 + a2 – 2ca·cosB
- c2 = a2 + b2 – 2ab·cosC
Proof of Law of Cosines
There are several ways to prove the law of cosine. Let us prove this using trigonometry. Consider the following figure.
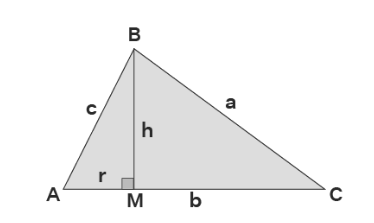


Derivation of Cosine Law
The following are the cosine law formulae for triangles with sides a, b, and c with angles A, B, and C.

Conclusion
When two sides and their enclosed angle are known, the law of cosines is useful for computing the third side of a triangle, as well as for computing the angles when a triangle’s all three sides are known.
 Profile
Profile Settings
Settings Refer your friends
Refer your friends Sign out
Sign out






