Profile
Settings
Refer your friends
Sign out
A conic section is a curve in mathematics that is formed by the intersection of the surface of a cone with a plane. Three types of conic sections exist. There are three types of parabolas: the parabola, the ellipse, and the hyperbola. Numerous key terms are used to describe these curves, including focus, directrix, latus rectum, locus, and asymptote. Let us take a closer look at the term “Latus Rectum” in this post.
A conic section is defined by a polynomial equation of second degree in two variables. Conic sections are classed as ellipses, parabolas, or hyperbolas. The various names for the conic section are derived from the fact that each conic section is represented by a cross-section of a plane cutting through a cone. Numerous essential terminology is employed to characterise these curves, including the latus rectum, focus, and directrix. The latus rectum of various curves such as a parabola, hyperbola, and ellipse will be discussed in detail in this article.
The latus rectum is the chord that runs parallel to the directrix in the conic section. The name latus rectum comes from the Latin words “latus” (side) and “rectum” (rectangle) (straight). The semi latus rectum is halfway between the latus rectum and the semi latus rectum. The illustration above illustrates the latus rectum of a parabola.
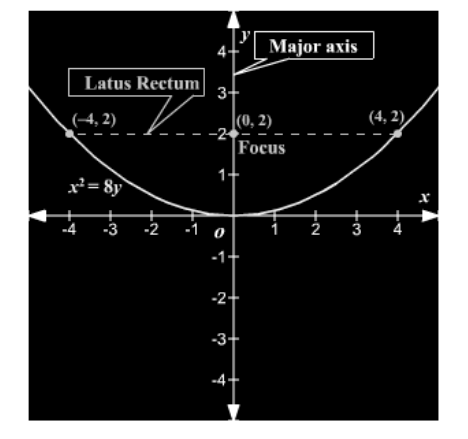
Latus Rectum
The term ‘latus rectum’ refers to the conic portion and is derived from the Latin words ‘latus’ which means side and rectum which means straight. The latus rectum is described as the chord that runs perpendicular to the directrix and passes through the focus. On the curve, the endpoint of the latus rectum is found. The semi latus rectum is thought to be half of the latus rectum. The length of the latus rectum is defined differently for each conic segment. For example,
- The length of the parabola’s latus rectum is always equal to four times the parabola’s focal length.
- The length of an ellipse’s latus rectum is defined as the square of the length of the conjugate axis divided by the length of the transverse axis.
- The length of a hyperbola’s latus rectum is defined as the square of the length of the transverse axis divided by the length of the conjugate axis.
- The length of a circle’s latus rectum is the same as the length of the circle’s diameter, and vice versa.
Focus
The focus ‘or’ foci are the fixed points upon which the conic sections are built. Ellipses and hyperbolas each have two foci, but circles and parabolas each have one.
Directrix
The directrix is a fixed-line that serves as the foundation for the construction of a conic section. Each point on the conic is positioned PF away from the focus and PM away from the directrix. The ratio of these distances, PFPM, is referred to as the conic’s eccentricity and defines its type.
Transverse Axis
The main axis of a conic section is the axis that passes through the foci and connects the vertices. This is sometimes referred to as the primary axis in the case of the ellipse.
Conjugate Axis
The conjugate axis is defined as the axis running through the centre and perpendicular to the transverse axis. This axis is referred to as the minor axis in the case of an ellipse.
Latus Rectum of a Hyperbola
The latus rectum of a hyperbola is a line that passes through the hyperbola’s foci and is perpendicular to the hyperbola’s transverse axis. A hyperbola’s latus rectum is also its focal chord, which is parallel to the ellipse’s directrix. Because the hyperbola has two foci, it has two latus rectums. The latus rectum of a hyperbola with the usual equation x2/a2 – y2/b2= 1 has a length of 2b2/a.
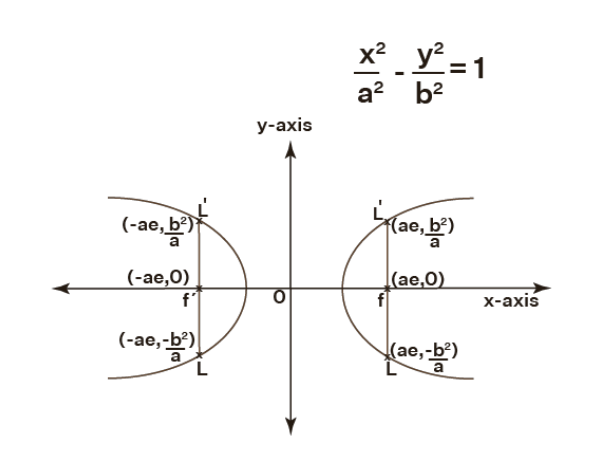
The extremities of the hyperbola’s latus rectum are (ae, b2/a) and (ae, -b2/a). And the endpoints of the hyperbola’s latus rectum are (-ae, b2/a) and (-ae, -b2/a). Here, ‘e’ denotes the hyperbola’s eccentricity, which is always more than one (e > 1). The latus rectum’s endpoints and the hyperbola’s focus are collinear, and the distance between the latus rectum’s endpoints equals the length of the latus rectum.
Conclusion
Specifically, the latus rectum is a term that refers to the conic area of the spine. It is necessary to first grasp what conic sections are in order to comprehend what a latus rectum is. Conic sections are two-dimensional curves that are formed when a cone meets a plane in a circular pattern. In mathematics, parabolas are classified into three types: parabolas, hyperbolas, and ellipses. Circles are a subset of the ellipse in terms of shape.
