Profile
Settings
Refer your friends
Sign out
Introduction:
Let f(t) is a function defined for all positive values of t. Then the Laplace Transforms of f(t) is given by L(f(t)) or f`(s) is defined as
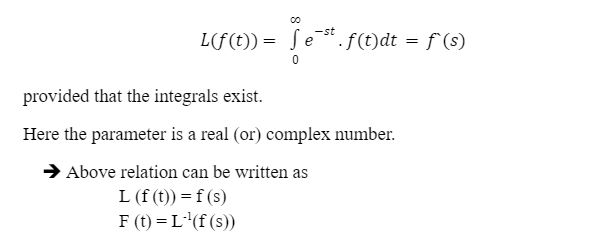
Sufficient conditions for the existence of Laplace Transform of a function:
The function f(t) must satisfy the following conditions for the existence of the Laplace Transform
- The function f(t) must be piecewise continuous in any limited intervals like 0 < a ≤ t ≤ b.
- The function f(t) is of exponential order like
F (t) ={t2, 0 < t < 5 or 2t, t > 5 is a piece – wise continuous for t > 0.
- F (t) = 1/t is not a piece – wise continuous in any intervals conditioning t = 0
- The function f(t) is said to be of exponential order ‘a’ if e e-atf(t) = 0 = finite quantity. F(t) = t2 , sin at, eat are of exponential order and continuous.
- F (t) = et2 is not of exponential order and its Laplace transform doesn’t exist.
Different Methods of Laplace Transform:
Laplace transform is an important part of control system engineering. To study and analyze the control system we have many different Laplace and inverse Laplace transform functions. The different types of methods that are used by control system engineers are
- Initial Value Theorem (IVT):
- It is the 1st basic property of Laplace transform.
- It is used to find the initial value at a time of a given function to transform without working hard to find f (t).
- Conditions for Initial Value Theorem:
- The function f (t) and its derivative should be Laplace transformable.
- If time t approaches 0+ then f (t) should exist.
- Conditions for Initial Value Theorem:
- If f (t) and f (s) are a pair. i.e. f (t)🡨 L 🡪f (s), then Initial Value Theorem is given by
ft= sFs=f(0+)
- Final Value Theorem (FVT):
- The final value theorem is used to find the solutions without knowing its function which inverse Laplace transforms.
- If both the functions are Laplace Transformable and g (f(s)) have no point on the axis then
gfs= f(t)
Properties of Laplace Transform:
- Linear Property:
If L (f (t)) = f(s) and L (g (t)) = g(s) then
L [c1 f (t) + c2 g (t)] = c1 (L (f (t))) + c2 (L (f (t))) = c1 f(s) + c2 f(s).
- First Shifting Theorem:
Periodic Function of Laplace Transform:
A function f (t) is said to be a periodic function if and only if f (t + T) = f (t) for some value of ‘T’. The small positive value of ‘T’ is called a period of the function.
Application of Laplace Transforms:
The Laplace Transform method is specially used for solving linear differential equations with constant coefficients.
Working Procedure:
- Take Laplace Transform to the both sides of the differential equation.
- Using following formula and initial conditions
L (f (t)) = f (s)
L (f `(t)) = s f (s) – f (0)
L (f“(t)) = s2 f (s) – s f (0) – f` (0)
L (f“` (t)) = s3 f (s) – s2 f (0) – s f` (0) – f“ (0)
- Transform the terms with minus signs to the right.
- Divide by the quotient of y (s) to get ‘y’ values in terms of ‘s’.
- Resolve this function of ‘s’ into partial fractions and take the inverse transform of both the sides, this result gives us y (t), which is the solution of the differential equation.
Disadvantages of Laplace Transform Method:
- It is only used to solve complex differential equations like great methods
- This method is only used to solve the differential equations using known constants.
- If the equation has unknown constants we cannot solve them using the Laplace Transform method.
Conclusion:
Laplace Transformation is a technique for solving differential equations. It is a shortcut method for solving differential equations. It provides a method to transform input function into output function. Many transformations exist like the Fourier Transformation. It is used to build blocks by controlling the engineering department.
