Jacobian is a term that refers to both a matrix and a determinant. Jacobian functions have a finite number of variables and the same number of functions. The functions are subjected to partial derivatives with respect to the variables and are organized in rows correspondingly. As with matrixes, Jacobian matrices come in a variety of configurations, including square matrices with the same number of rows and columns and rectangular matrices with the same number of rows and columns.
Jacobian Matrix
Matrices have a distinctive representation and come in a variety of sizes and shapes. Matrices can be classed according to their ranks, order, and content. We encountered various forms of matrices in high school, each with its own set of parameters. Matrixes aid in the simplification of calculations; thus, even the most complex calculations performed by computers are first broken down into matrices and then solved. To comprehend the Jacobian Matrix, it is necessary to grasp vector calculus and some of the features of Matrices.
As noted previously, the Jacobian matrix is derived from the partial derivatives of its variable-dependent functions. The term Jacobian is often used to refer to the Jacobian matrix’s determinant. This matrix contains all vector functions’ partial derivatives. Now the issue becomes, what use does the Jacobian matrix serve? Jacobian is used for a variety of applications, including determining the Jacobian transformation of coordinates and differentiation with coordinate transformation.
Jacobian Determinant
If the Jacobian matrix is a square matrix, the rows and columns are equal; so, m = n; and f is a function from Rn to itself. We can get a determinant, dubbed the Jacobian determinant, from the Jacobian matrix. The Jacobian determinant is occasionally referred to as “Jacobian.”
At a given location, the Jacobian determinant contains critical information about f’s behavior around that point. If the Jacobian determinant is greater than zero at p, then the continuously differentiable function f is invertible near the point p Rn. This is the theorem of the inverse function. Additionally, if the Jacobian determinant at p is positive, f keeps orientation near p. Similarly, if f is negative, it reverses direction. The absolute value of the Jacobian determinant at p is used in the general substitution rule because it indicates by what factor the function f expands or contracts volumes near p. When evaluating numerous integrals of a function across an area inside its domain, the Jacobian determinant is used. To account for the change in coordinates, the amount of the Jacobian determinant appears as a multiplicative component within the integral. This is because the n-dimensional dV element (parallelepiped in the new coordinate system) is the determinant of the edge vectors of a parallelepiped. The Jacobian matrix is used in disease modeling to determine the stability of the disease-free equilibrium.
Characteristics of a Jacobian Matrix
A Jacobian matrix is a matrix of any shape that holds a vector function’s first-order partial derivative. The different versions of the Jacobian matrix are rectangular matrices with non-identical rows and columns, and square matrices with equal rows and columns. The following is a more rigorous mathematical depiction of a Jacobian matrix.
f: Rn→Rm is a function that accepts the vector x Rn as an input and returns the vector f(x) Rm as an output. As a result, f’s Jacobian matrix J is a mXn matrix.
Typically, variable x is the matrix’s entry. This is critical to understand since it demonstrates that the function is differentiable at the point x. The fact that a matrix is differentiable at a point indicates that it can be mapped and given a geometric and visual method to comprehend the underlying equations. The most common types of Jacobian matrices are polar-Cartesian and spherical-Cartesian. These matrices are critical because they facilitate the conversion of one coordinate system to another, which is valuable in a wide variety of mathematical and scientific endeavors.
The Jacobian matrix plays a significant role in all branches of mathematics, science, and engineering. One prominent application is in the field of control engineering, where the employment of Jacobian matrices enables the local (approximate) linearization of nonlinear systems around a specified equilibrium point, enabling the application of linear systems techniques such as eigenvalue computation (and thus allowing an indication of the type of the equilibrium point). Jacobian matrices are also utilized to estimate the internal states of nonlinear systems when an extended Kalman filter is constructed. To summarise, Jacobian matrices have a truly unique and significant place in the world of matrices!
Inverse
According to the inverse function theorem, the matrix inverse of an invertible function’s Jacobian matrix equals the inverse function’s Jacobian matrix. That is, if the Jacobian of the function f: Rn→ Rn is continuous and nonsingular at the point p in Rn, then f is invertible in some neighborhoods of p.
Jf-1 = Jf-1
Conversely, if the Jacobian determinant is not zero at a point, the function is locally invertible near this point; that is, the function is invertible in a neighborhood of this point.
The (unproven) Jacobian conjecture is linked to global invertibility for polynomial functions, that is, functions defined by n polynomials in n variables. It argues that if the Jacobian determinant is not zero (or, more precisely, if it lacks any complex zero), the function is invertible and its inverse is a polynomial function.
Conclusion
A Jacobian matrix is a matrix composed entirely of partial derivatives. The Jacobian matrix’s determinant is called the jacobian matrix. The matrix will contain all of the vector function’s partial derivatives. Jacobian is mostly used in coordinate transformations. It discusses differentiation using coordinate transformations.
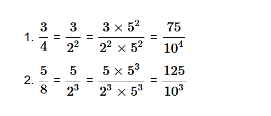
For the decimal expansion of repeating rational numbers, the following theorem can be stated.
Theorem 3: If n is a rational number that can be expressed as the ratio of two integers j / k and the prime factorization of k does not take the form of 2x 5y, where x and y are non-negative integers, then x has a repeating decimal expansion.
Check out the following rational number to decimal examples to help you understand:
3/7 = 0.4285714285714. . . . . . . . . . = 0.43.
9/13 = 0.6923076. . . . . . . . . . . = 0.69.
Important points:
- The term “terminating decimal expansion” refers to the fact that the decimal representation or expansion ends at a given number of digits.
- Even if the repetition begins after a given number of digits, any non-terminating yet recurring decimal representation corresponds to a rational integer
- If a number can be represented as p/(2n5m), with p ∈ Z and m,n ∈W, then the rational number is a terminating decimal.
 Profile
Profile Settings
Settings Refer your friends
Refer your friends Sign out
Sign out






