Profile
Settings
Refer your friends
Sign out
An involute (also known as an evolvent) is a form of curve in mathematics that is dependent on another shape or curve. The location of a point on a taut string as it is either unwrapped from or wrapped around a curve is called an involute of a curve. It’s a type of curve that belongs to the roulette family of curves. The original curve is the evolute of an involute. In his work Horologium oscillatorium sive de motu pendulorum ad horologia aptato demonstrationes geometricae, Christiaan Huygens developed the concepts of involute and evolute of a curve (1673).
Definition of involute:
the locus of a point in the plane of a curve that is regarded to be the end of a taut string being unwound from that curve.
Involutes of the Curves:
The involutes of the various involute curves are as follows:
i) Circle Involute
ii) Catenary Involute
iii) Deltoid Involute
iv) Parabola Involute
v) Ellipse Involute
i) Circle Involute:
The route drawn out by a point on a straight line that rolls around a circle is known as the involute of a circle. Huygens looked at it while he was thinking of clocks without pendulums that may be used on ships at sea.
The involute’s parametric equation is as follows:
xi = a(cost + tsint)
yi = a(sint – tcost)
Here ‘a’ is the radius and ‘t’ is the parameter angle in the median.
ii) Catenary Involute:
The catenary is a completely flexible chain hanging by its ends and influenced by gravity. In 1691, Leibniz, Huygens, and Johann Bernoulli discovered its equation. They were responding to Jacob Bernoulli’s challenge to find the equation for the ‘chain-curve.’
the parametric equation of the involute as
xi = t – tanh t
yi = sech t
As a result, the involute is half of a tractrix.
iii) Deltoid Involute:
A deltoid curve, also called a tricuspoid curve or a Steiner curve, is a three-cusped hypocycloid. In other words, it’s the roulette formed by a point on a circle’s perimeter rolling along the interior of a circle with three or one-and-a-half times its radius without slipping.
The involute of the deltoid is
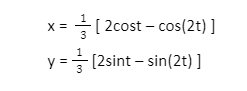
iv) Parabola Involute:
The involute of a curve is obtained by connecting one end of a taut string to the curve and winding the thread onto the curve while following the course of the string’s free end.
The involute of a parabola is given by
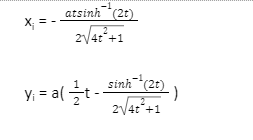
v) Ellipse Involute:
Involute or evolvent is the locus of the free end of this string. The evolute of an involute of a curve is referred to that original Four normal vectors can be drawn to the ellipse from a point inside the evolute, three normal vectors from a precise point on the evolute, and only two normal vectors from a point outside the evolute.
The involute of an ellipse is given by the parametric equations
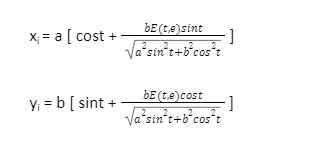
Where ‘E’ is an elliptic integral of the second kind, and ‘e’ is the eccentricity.
How to draw involute:
Step 1: Draw some tangents to the point given on the curve.
Step 2: Select two adjacent lines.
Step 3: extend lines in opposite directions.
Step 4: Now get the intersection point.
Step 5: After that, let the endpoint as center.
Step 6: Calculate the distance between the provided centre and the 1st tangent’s point.
Step 7: Now draw an arc.
Step 8: Let P1 and P2 be two successive tangents, as illustrated in the diagram.
Let X be the point of intersection and XB the radius.As a result, the arc BB1 has been obtained.
Step 9: Let’s look at two more neighbouring tangents, P2 and P3.
Step 10: Assume that Y is the centre of their intersection.
Step 11: Assume that YB1 is the radius.
Step 12: Make an arc. B1B2
Step 13: Continue with the same procedure for the remaining tangents. We’ll be able to make a curve out of these arcs . And now we have the curve’s involute.
Application of involute:
- i) The curve’s involutes can be used in a variety of industries and enterprises.
- ii) To create teeth for two revolving machines and gears in the gear industry.
Real life example:
In a project there was a computerized sewing machine. It has used Involute as a Cam follower structure to convert the rotational motion of a needle to convert it to translational motion of a needle.
Conclusion:
An involute (also known as an evolvent) is a form of curve in mathematics that is dependent on another shape or curve. The location of a point on a taut string as it is either unwrapped from or wrapped around a curve is called an involute of a curve.
