Introduction
Inverse trigonometric functions are closely related to fundamental trigonometric functions as a learning topic. The domain and range of inverse trigonometric functions are translated from the domain and range of trigonometric functions
Inverse trigonometric functions are the inverse functions of basic trigonometric functions. Sin-1 x = θ can be substituted for the basic trigonometric function sin θ = x. can take the form of whole integers, decimals, fractions, or exponents in this case. We obtain θ = sin-1 (1/2) for θ = 30°, where lies between 0° and 90°. Inverse trigonometric function formulas can be made from any trigonometric formula. Inverse trigonometric functions such as arcsin(x), arccos(x), arctan(x), arccsc(x), arcsec(x), and arccot are written with an arc-prefix (x). To get the angle of a triangle from any of the trigonometric functions, utilize the inverse trigonometric functions. It’s employed in a variety of professions, including geometry, engineering, and physics.
Inverse trigonometric function example is x = sin-1y.
Formulas of Inverse Trigonometric
The following formulas have been combined together to provide a list of inverse trigonometric formulas. These formulas can be used to transform one function to another, as well as to determine the functions’ results. Inverse trigonometric functions can be used to calculate principal angle values and to perform a number of arithmetic operations. Furthermore, all basic trigonometric function formulas have been transformed to inverse trigonometric function formulas and are divided into four categories below.
- Arbitrary Values
- Reciprocal and Complementary functions
- Sum and difference of functions
- Double and triple of a function
For Arbitrary Values
- sin-1(-x) = -sin-1x,x ∈ [-1,1]
- tan-1(-x) = -tan-1x, x ∈ R
- cosec-1(-x) = -cosec-1x, x ∈ R – (-1,1)
- cos-1(-x) = π – cos-1x, x ∈ [-1,1]
- sec-1(-x) = π – sec-1x, x ∈ R – (-1,1)
- cot-1(-x) = π – cot-1x, x ∈ R
Reciprocal and Complementary Function
- sin-1x = cosec-11/x, x ∈ R – (-1,1)
- cos-1x = sec-11/x, x ∈ R – (-1,1)
- tan-1x = cot-11/x, x > 0
- tan-1x = – π + cot-1 x, x < 0
- sin-1x + cos-1x = π/2, x ∈ [-1,1]
- tan-1x + cot-1x = π/2, x ∈ R
- sec-1x + cosec-1x = π/2, x ∈ R – [-1,1]
Sum and Difference of Function
- sin-1x + sin-1y = sin-1(x.√(1 – y2) + y√(1 – x2))
- sin-1x – sin-1y = sin-1(x.√(1 – y2) – y√(1 – x2))
- cos-1x + cos-1y = cos-1(xy – √(1 – x2).√(1 – y2))
- cos-1x – cos-1y = cos-1(xy + √(1 – x2).√(1 – y2))
- tan-1x + tan-1y = tan-1(x + y)/(1 – xy), if xy < 1
- tan-1x + tan-1y = tan-1(x – y)/(1 + xy), if xy > – 1
Double and Triple of Function
- 2sin-1x = sin-1(2x.√(1 – x2))
- 2cos-1x = cos-1(2x2 – 1)
- 2tan-1x = tan-1(2x/1 – x2)
- 3sin-1x = sin-1(3x – 4x3)
- 3cos-1x = cos-1(4x3 – 3x)
- 3tan-1x = tan-1(3x – x3/1 – 3x2)
Graph of Inverse Trigonometric Functions
The graphs of several inverse trigonometric functions with their range of principal values can be plotted. In the domain of corresponding inverse trigonometric functions, we have picked random values for x. In the following sections, we’ll learn about the domain and range of these functions.
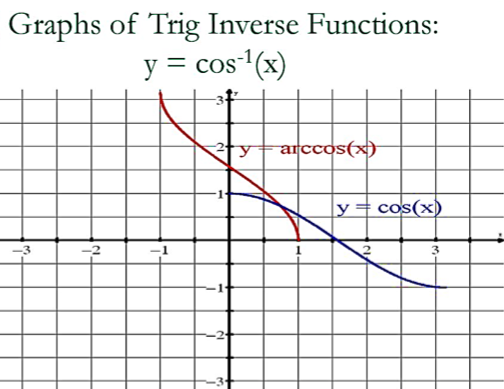
Figure: 1 Graph of Inverse Trigonometric Functions
Arcsine function
The arcsine function, also known as the inverse sine function or sin-1 x, is the inverse of the sine function as a mathematical function. The sine inverse function graph is shown below. The inverse function of the sine is the arcsine (notation: arcsin or sin-1). That is to say: Formula for arcsin
Because the arcsine and sine functions are inverse, their combination is the same. That is to say:
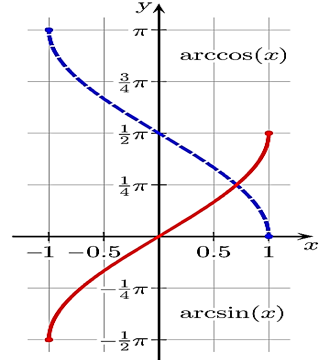
Figure: 2 Arcsine function graph
Conclusion
In the fields of engineering, construction, and architecture, inverse trigonometric ratios are frequently used. We use inverse trigonometric ratios because they are the simplest way to find an unknown angle. In situations where we need to know the angle for our aid and need to get the information quickly. Inverse trigonometric ratios are used in the following situations: This formula is used to calculate the unknown angles of a right-angled triangle It’s used to figure out how deep a hole is or what angle it’s inclining at. Architects use it to calculate the angle of a bridge and its supports. This tool is used by carpenters to obtain a precise cut angle.
 Profile
Profile Settings
Settings Refer your friends
Refer your friends Sign out
Sign out






